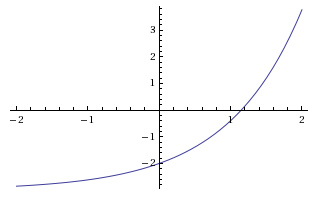
State the domain, range, and horizontal asymptote for the given exponential function: f(x) = [2.6]^x − 3.

 

A.

Domain: (-∞, ∞)
Range: (-3, ∞)
Horizontal Asymptote: none

Incorrect. The exponential graphs of the form f(x) = a* b^x + c always have a horizontal asymptote.
B.

Domain: (-∞, ∞)
Range: (-3, ∞)
Horizontal Asymptote: y = -3

Correct! You found the lower range limit and horizontal asymptote even though it wasn’t drawn on the graph.

C.

Domain: (-∞, ∞)
Range: (-2.6, ∞)
Horizontal Asymptote: y = -2.6

Incorrect. The base value of 2.6 doesn’t affect the domain or range in the problem. Focus on the vertical shift of -3 and try again.

D.

Domain: (-2, ∞)
Range: (-3, ∞)
Horizontal Asymptote: y = -3

Incorrect. Although the picture does not show it, exponential graphs always have an infinite domain.

Given f(x) = 3*2^(x - 2), state the domain, range, and horizontal asymptote for f(x).

A.

Domain: (-∞, ∞)
Range: (0, ∞)
Horizontal Asymptote: none

Incorrect. The exponential graphs of the form f(x) = a* b^x + c always have a horizontal asymptote.
B.

Domain: (-∞, ∞)
Range: (2, ∞)
Horizontal Asymptote: y = 0

Incorrect. The range is not affected by the base 2. The range can only be affected by a vertical shift, which this function does not have.

C.

Domain: (-∞, ∞)
Range: (0, ∞)
Horizontal Asymptote: y = 0

Correct! You found the lower range limit and horizontal asymptote even though it wasn't drawn on the graph.

D.

Domain: (0, ∞)
Range: (0, ∞)
Horizontal Asymptote: y = 0

Incorrect. Remember the domain is infinite for exponential functions.

Given f(x) = [-2 * 3]^(x − 2) + 5, state the domain, range, and horizontal asymptote for f(x).

A.

Domain: (-∞, ∞)
Range: (-∞, 5)
Horizontal Asymptote: y = 5

Correct! You found the proper upper range limit and horizontal asymptote.

B.

Domain: (-∞, ∞)
Range:(-∞, 5)
Horizontal Asymptote: y = 0

Incorrect. A vertical shift of 5 units causes the horizontal asymptote to shift up 5 units as well.

C.

Domain: (-∞, ∞)
Range: (5, ∞)
Horizontal Asymptote: y = 5

Incorrect. Multiplying by -2 turned the exponential function upside down and changed the range.

D.

Domain: (-∞, ∞)
Range: (5, ∞)
Horizontal Asymptote: y = 0

Incorrect. A vertical shift of 5 units causes the horizontal asymptote to shift up 5 units as well. Also, multiplying by -2 turned the exponential function upside down and changed the range.

Given f(x) = 4^(x − 1) + k has a horizontal asymptote at y = 3, what must be the value for k?

A. k = -3
Incorrect. This would cause a horizontal asymptote at y = -3.

B. k = 1
Incorrect. This would cause a horizontal asymptote at y = 1. The exponent (x − 1) has nothing to do with the horizontal asymptote.

C. k = 3
Correct! The function f(x) = 4^(x − 1) + 3 has a horizontal asymptote at y = 3 caused by the vertical shift of 3 units.

D. Not enough information
Incorrect. There is enough information. The horizontal asymptote helps you decide on the proper vertical shift.

Given f(x) = a * 2^x - 3 has a range of (-∞, -3), what could be the value of a?

A. a = -3
Correct! The -3 causes the graph to reflect across the x-axis.

B. a = 0
Incorrect. If a = 0, the function would become f(x) = -3, which is a horizontal line with range only at the value of -3.

C. a = 2
Incorrect. If a is any positive value, the function would increase without bound, causing a range of (-3, ∞), not (-∞, -3) as stated in the problem.

D. a = 3
Incorrect. If is any positive value, the function would increase without bound, causing a range of (-3, ∞), not (-∞, -3) as stated in the problem.