You and your fiancé are shopping for a diamond to purchase for your engagement ring. You have done your research online and know that the cost of a diamond depends upon its weight, in carats. The cost, C, of a diamond weighing w carats can be found using the exponential model C = 795(1.33)w. You have your heart set on a diamond that weighs 2.2 carats. Using the exponential function, find the cost of that diamond.
- $1,488.82

Correct! On the calculator’s home screen 2.2 is substituted in for w into the exponential function, C=795(1.33) to the power of w, the cost of the diamond, rounded to the nearest penny is $1,488.82.
- $2,3226.17

Incorrect. The equation was entered into the calculator incorrectly, 2.2 is a factor in a product rather than the exponent.
- $2,268.76

Incorrect. The equation was entered into the calculator incorrectly; the growth rate for the exponential function is 2.2.
- There is not enough information to find the cost of the diamond.
Incorrect. To find the cost of the diamond substitute 2.2 in for w, the weight in carats, into the given exponential function and evaluate the expression.
Jenn is cramming for an important final math exam. She wants to stay up late to study, so she drinks a lot of caffeine and eats chocolate candy, consuming 500 mg of caffeine. 350 mg of caffeine is considered a moderate level and the body eliminates caffeine at the rate of 15% per hour. How long will it take for the caffeine level in Jenn's body to reach a moderate level? (Round your answer to the nearest tenth of an hour.)
- 2.0 hours
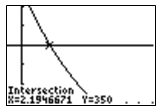
Incorrect. The functions were correctly entered into the calculator and the intersection was found using features on the calculator. However, the answer was to be rounded to the nearest tenth of an hour.
- 2.2 hours
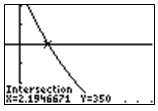
Correct! The functions were correctly entered into the calculator, the intersection was found using features on the calculator and rounded to the nearest tenth.
- 0.2 hours
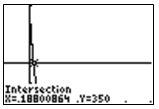
Incorrect. The Y squared function does not show the correct decay rate.
- 0.1 hours
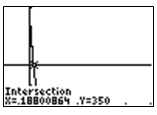
Incorrect. Change squared to 2; the exponential function in Y2 does not show the correct decay rate.
Walter invested $2500 into a retirement account. The exponential function below shows the amount of money, A, that will be in his account at the end of t years.
A = 2500(1 + r)t
Walter's account pays an annual interest rate of 6%. Assuming he does not touch this money, how much will be in his account at the end of 4 years? Round your answer to the nearest dollar.
- $1,952
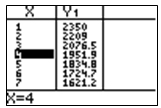
Incorrect. The function was entered into Y1 at a decay rate (1 -.06) instead of at a growth rate of (1 +.06).
- $2,978
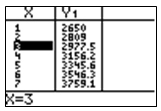
Incorrect. The function was entered correctly into Y1. The table was used to determine the amount of money in the account but the wrong entry in the table was used.
- $3,156
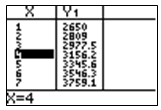
Correct! The function was entered correctly into the function and the table values were used to determine the amount of money in the account after 4 years.
- $2,525
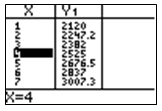
Incorrect. The function was entered into the calculator correctly. The initial investment was $2500, not $2000.
The area of a wound decreases exponentially over time. After t days, the area, A, of a wound can be modeled by the function, A = We-0.05t , where W represents the area of the original wound. Find what the size of the original wound was if after 2 weeks the wound reduced in size to 3 cm2. Round your answer to the nearest hundredth.
- 3.32cm2
Incorrect. 3 was substituted in for A but 2 was incorrectly substituted in for t. [Since t is the number of days, convert 2 weeks to 14 days.]
- 6.04cm2
Correct! Given the function A = W times e to the power of -0.05t, 3 was substituted in for “A” and 14 was substituted in for “t” then the equation can be solved algebraically for “W.”
- 1.49cm2
Incorrect. Given the function A = W times e to the power of -0.05t, 3 was incorrectly substituted in for W.
- 2.71cm2
Incorrect. Given the function A = W times e to the power of -0.05t, 3 was incorrectly substituted in for W and 2 was incorrectly substituted for t. (Since t is the number of days, convert 2 weeks to 14 days.)










