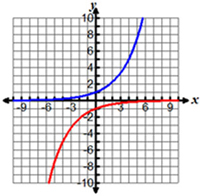
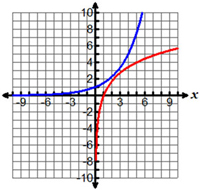
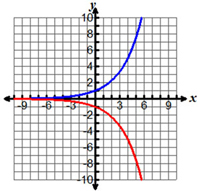
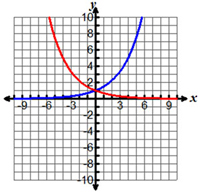
Which of the following graphs shows an exponential graph and its inverse?
A.
 |
B. |
C. |
D. |
The restricted domain and range for an exponential function are given below.
Domain: {x│x ≥ 1}
Range: {y│y ≥ 3}
Which of the following describes the domain and range of its inverse?
What is the domain, range and vertical asymptote for f(x) = log3(x − 5) + 2?
Below are some characteristics of an exponential function.
Based on this information, what is the value of k?
Christina plans to purchase a modular building for her new business priced at $60,000. Since this building will depreciate by 5% each year, she knows that the function for this situation can be modeled by V = 60,000∙(0.95)t where V represents the value of the building over t years.
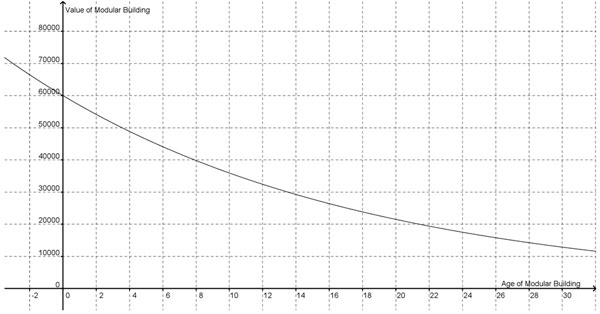
If the graph above represents this situations, solve the equation 40,000 = 60,000∙(0.95)t.
Which of the following equations is the first step for solving the equation 9(x + 1) = 272x using same bases?
Solve log4(x − 6) + log4(2x) = log4x for x.
What is the value of x in the equation log8x = four-thirds 4 3 ?
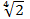
What is the value of x in the equation log8(x + 5) + log3(2x) = log328?
Use a graphing method or table method to solve the inequality 25(2.1)x > 50.
Recent research has placed Atascocita as the fastest growing city in Texas. According to Bloomberg Business, this city has shown a yearly increase of 8% since 2009.If Atascocita continues to grow at this rate, which exponential equation could be used to determine its population in 2012 assuming the population in 2009 was 40,947.(
Iodine-123 is used to diagnose thyroid disease. Its half-life is about 13 hours as modeled by the formula A = A0*0.5t/13 where A0 represents the initial amount and A represents amount after t hours. Suppose you begin with a sample of 15 grams, how long will it take to decay to 3 grams?
The table below shows the average daily number of vehicles that commute into the city of Metropolis for a 7 year period.
| Year | Average Number of Vehicles Daily |
|---|---|
| 2004 | 79,167 |
| 2005 | 95,000 |
| 2006 | 114,000 |
| 2007 | 136,800 |
| 2008 | 164,160 |
| 2009 | 196,992 |
| 2010 | 236,390 |
The city council decided that once the number of vehicles reaches 550,000, the city will begin to implement a commuter bus system. Find an exponential growth model that fits the data. Then use the model to approximate the year the city will implement a commuter bus system.
Below is a graph of an exponential function and its asymptote.
Which table represents values of its inverse?
A.
|
B.
|
||||||||||||||||
C.
|
D.
|
The graph below shows the function f(x) = 4x − 2, where x ≥ 0.
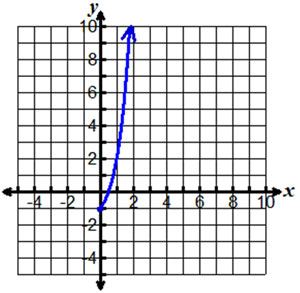
Which of the following correctly shows the range of the inverse of this function?
State the domain, range and horizontal asymptote for the exponential function f(x) = 2*5(x - 1) + 3.
A log function in the form y = logb(x + c) + d has been graphed below.
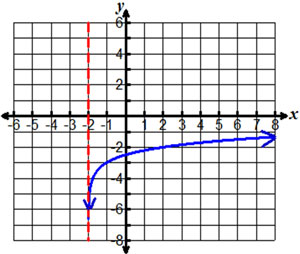
Based on this graph, which of the following best describes the domain, range and asymptote?
The table below represents the equation y = 3 * 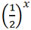
| x | y |
|---|---|
| -3 | 24 |
| -2 | 12 |
| -1 | 6 |
| 0 | 3 |
| 1 | three-halves 3 2 |
| 2 | three-fourths 3 4 |
| 3 | three-eighths 3 8 |
| 4 | three-sixteenths 3 16 |
| 5 | three-thirty-secondths 3 32 |
Based on this table, which of the following is a solution to the equation 3 = 3 * 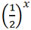
Which of the following could be the first step for solving the equation 5(x + 2) = 3000?
Robert plans to solve the equation log3(x2 − 25) − log3(x − 5) = log3 (2x − 1) using the table and/or graphing method on his calculator. Which of the following screen shot is a correct input to solve this equation?
A.
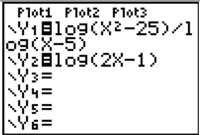 |
B.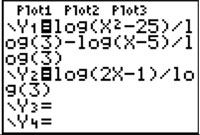 |
C.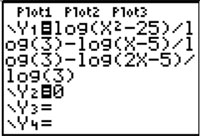 |
D. |
The formula used to calculate the amount money, A, in an a savings account after t years is A = P(1 + r)t, where P is the principal (or initial amount) and r is the interest rate. Mrs. Gonzalez is trying to determine how long it would take her savings account to double in value. If the interest rate is 4.5% and Mrs. Gonzalez does not make any additional deposits or withdraws, which of the following equations will determine how long it will take her money to double?
A biologist is observing a strain of bacteria that is growing exponentially in a Petri dish. If one bacteria took an hour to divide into 2 bacteria, which inequality will determine how long will it take for 20 bacteria in the disk to grow to at least 5000?
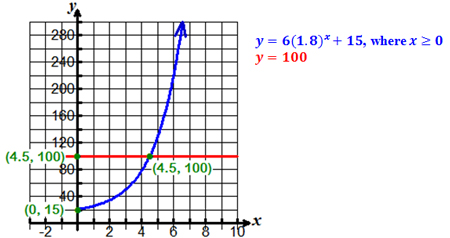
Use the graph below to solve the inequality 6(1.8)x + 15 < 100?
According to statistics, the growth of the population age 65 and older has grown exponentially since the year 1900. The equation y = 3∙ 1.024x represents the approximate growth of this population in millions, where x = 0 represents the year 1900; x = 1 represents the year 1901; and so on. Using this formula, predict the population in the year 2030.
What is the domain of the equation log7(15 − 3x) − log7(x − 2) = log7x?