What is the solution to the inequality x + 3 x − 4 ≥ 0 ?

A. -3 ≤ x < 4
Incorrect. This would be the solution if the equation were less than or equal to 0 instead of greater than or equal to 0.

B. x > 4
Incorrect. This answer is only partially correct. Examine the graph of the left side of the inequality again.

C. x ≤ -3 or x > 4
Correct! The graph of the rational function shows the function is greater than or equal to 0 when x is less than or equal to -3 and again when x is greater than 4.

D. x ≤ -3 or x ≥ 4
Incorrect. 4 cannot be in the solution to this inequality.

What is the solution to the inequality 3 x + 4 − 1 x − 2 ≤ 0 ?

A. x < -4 or 2 < x ≤ 5
Correct! Graph the equation. The graph clearly shows the expression is less than 0 when x is less than -4 and when x is greater than 2 and less than or equal to 5.

B. -4 < x < 2 or x ≥ 5
Incorrect. You solved for when the expression on the left is greater than or equal to 0.

C. x < -4 or 2 < x < 5
Incorrect. While this solution is almost correct, x = 5 needs to be included in the solution since it makes the rational expression on the left equal to 0.

D. x < -4 or 0 ≤ x < 2
Incorrect. Check the left side of the inequality.

What is the solution to the inequality x² + 10 x² + 16 < 0 ?

A. x ≥ 5 8
Incorrect. Five eighths is the y-intercept, it is not part of the solution to the inequality.

B. -4 < x < 4
Incorrect. The denominator was changed to x² − 16.

C. All real numbers
Incorrect. This inequality is never less than zero.

D. No solution
Correct! The graph on the left is always greater than the graph on the right therefore there are no solutions to this inequality.

According to the following graph, for what values of x is 1 x − 2 − 1 x + 2 ≥ 3 x² − 4 ?

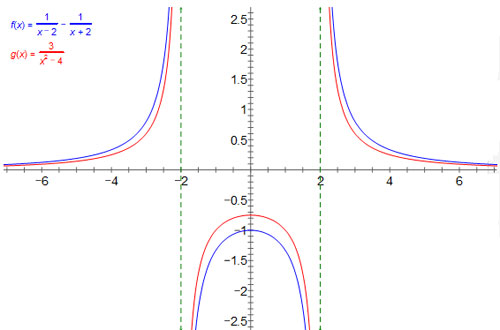
A. -2 ≤ x ≤ 2
Incorrect. In that interval, the left side of the inequality is less than the right side.

B. x ≤ -2 or x ≥ 2
Incorrect. The intervals are correct except x cannot equal 2 or -2.

C. x < -2 or x > 2
Correct! To solve this inequality, we are looking for when the blue graph (left side) is above the red graph (right side). This is true to the left of -2 or to the right of 2.

D. -2 < x < 2
Incorrect. In that interval, the left side of the inequality is less than the right side.