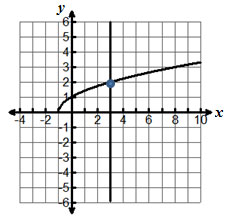
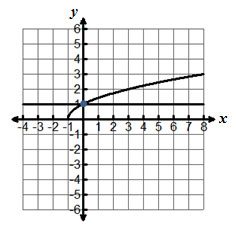
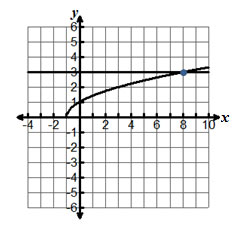
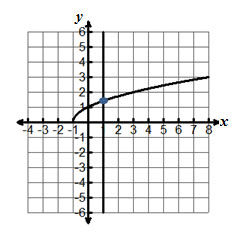
Which of the following is the inverse function for f(x) = √ x - 3, x ≥ 3?
A. f -1(x) = x + 3, x ≥ 0
Incorrect. To eliminate a square root, square each side.
B. f -1(x) = x2 + 3, x ≥ 0
Correct! This is the inverse equation.
C. f -1(x) = x2 - 3, x ≥ 3
Incorrect. To eliminate a minus 3, perform the inverse operation.
D. f -1(x) = y + 3, y ≥ 0
Incorrect. To get the inverse function, first switch the x and y. Also remember that f(x) represents the y-values.
Domain: {x|x≥5}
Range: {y|y≥3}
Which of the following describes the domain and range of its inverse?
A. Domain: {x|x≥5}; Range:{y|y≥3}
Incorrect. Think about what happens to the domain and range when a function is reflected over y=x.
B. Domain: {x|x≥-5}; Range: {y|y≥-3}
Incorrect. You switched the signs. Try switching the x- and y-values.
C. Domain: {x|x≥3}; Range: {y|y≥5}
Correct! Switching the domain and range yields the domain and range of its inverse.
D. Domain: {x|x≤3}; Range: {y|y≤5}
Incorrect. Only the x- and y-values switch, not the inequality signs.
3 = √x+1
A.  |
B.  |
C.  |
D.  |
A
Incorrect. The square root is graphed correctly. Since you want to know the common x-value when y is 3, the second equation should be y = 3.
B
Incorrect. The square root is graphed correctly. Set each side equal to y to find x.
C
Correct! This point tells us the x-value of the two expressions 3 and the square root of ( x + 1).
D
Incorrect. The square root is graphed correctly. Set each side equal to y to find x.

A
Incorrect. You did the left side of the equation correctly. Now you should perform the same operation to the right side.
B
Incorrect. You should eliminate the radical before solving for x.
C
Incorrect. You did the left side of the equation correctly. Now you should perform the same operation to the right side.
D
Correct! You squared both sides of the equation to eliminate the radical.
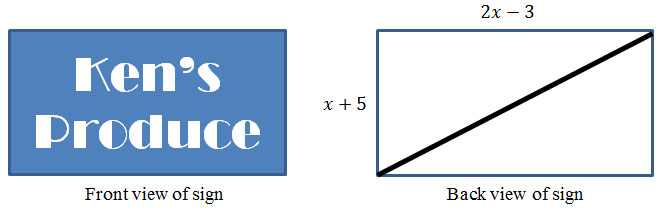
Which equation best describes the length, y, of this diagonal?
A. y = √5x2 + 34
Incorrect. You used the correct formula (Pythagorean Theorem), but you squared your binomials incorrectly.
B. y = √5x2 + 34
Correct! Using the Pythagorean Theorem, this is the length of the diagonal.
C. y = √3x2 − 22x − 16
Incorrect. You used the correct formula (Pythagorean Theorem), but the diagonal should be the c in the formula.
D. y = 2x2 + 2x − 15
Incorrect. You used the area formula. Since the diagonal creates two right triangles, think about what formula will find the length of a side of a right triangle.
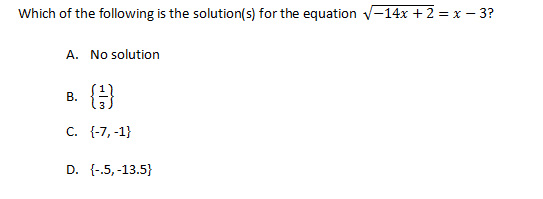
A
Correct! Both -1 and -7 are extraneous solutions.
B
Incorrect. You forgot to square the binomial x − 3.
C
Incorrect. Your algebraic steps are correct. Now check your solutions.
D
Incorrect. Don’t forget to FOIL when squaring a binomial.
| x | y |
| 2 | -1 |
| 3 | 0 |
| 4 | 1 |
| 7 | 2 |
| 12 | 3 |
| 19 | 4 |
| 28 | 5 |
| 39 | 6 |
Based on this information, what is the solution of √x - 3 < 3?
A. [3, 12)
Correct! The y-values represent the square root expression. These y-values are less than 3.
B. (12, ∞)
Incorrect. The y-values represent the square root expression. These y-values are greater than or equal to 3.
C. [2,7)
Incorrect. The y-values represent the square root expression. 2 is not part of the domain.
D. (-∞, 12)
Incorrect. The y-values represent the square root expression. Not all of these x-values are part of the domain.
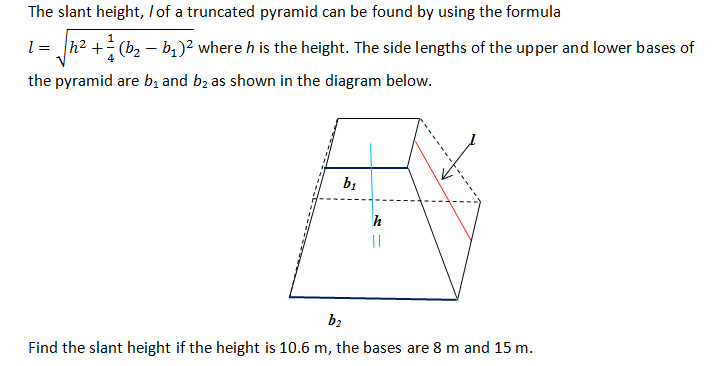
A. 10.5 m
Incorrect. You forgot to square the difference of the bases.
B. 3 m
Incorrect. You forgot to square the height and the difference of the bases.
C. 11.2 m
Correct! This is the slant height.
D. 12.7
Incorrect. You should multiply the difference of the bases by 1/4 before you take the square root.
Which table represents the values of its inverse?
A. 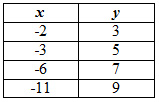 |
B. 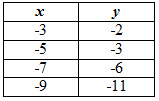 |
C. 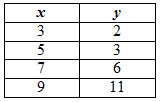 |
D. 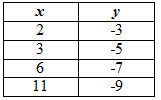 |
A
Incorrect. This is a reflection over the x-axis. Think about what happens to the coordinates when finding the inverse of a function.
B
Incorrect. This is a reflection over the line y = -x. You are looking for a reflection over the line y = x.
C
Correct! Switching the x- and y-coordinate produces the inverse of a function and reflects over the line y = x.
D
Incorrect. This is a reflection over the y-axis. Think about what happens to the coordinates when finding the inverse the inverse of a function.
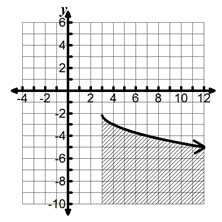
Which inequality is represented by this graph?
A. y < -2 − √x − 3
Incorrect. Notice that the boundary is included in the graph.
B. y > -2 − √x − 3
Incorrect. Notice that the boundary is included and the area less than the function.
C. y ≥ -2 − √x − 3
Incorrect. Pick a point in the shaded region and substitute into this inequality to see if it produces a true statement.
D. y ≤ - 2 − √ x − 3
Correct! The graph represents the square root function and the area below.

Which of the following inequalities describes the dimensions of the base of the box?
A
Incorrect. You used the correct formula (Pythagorean Theorem), but the hypotenuse should be the length of the wand.
B
Incorrect. Remember that you are looking for a length that describes a distance between two numbers. These inequality signs do not describe a value between two quantities.
C
Incorrect. You set up your equation correctly, but recall that the factors of a^2-b^(2 ) are (a+b)(a-b).
D
Correct! To determine the length of y, use the length of the wand as the hypotenuse when calculating using the Pythagorean Theorem.
|
x |
y |
|
-1 |
0 |
|
0 |
-2 |
|
1 |
-2.828 |
|
2 |
-3.464 |
|
3 |
-4 |
|
4 |
-4.472 |
|
5 |
-4.899 |
|
6 |
-5.292 |
Based on this information, what is the solution for -2√x + 1 = -4?
A. {-4}
Incorrect. You are looking for an x-value that will produce a y-value of -4.
B. {3}
Correct! An x-value of 3 produces a y-value of -4.
C. {6}
Incorrect. You are looking for an x-value that will produce a y-value of -4.
D. No solution
Incorrect. You are looking for an x-value that will produce a y-value of -4.
A. d = √5w2 − 8w + 13
Correct! Using the distance formula or the Pythagorean Theorem will give you the needed distance.
B. d = √3w2 −16w + 5
Incorrect. If you used the Pythagorean Theorem, these vertical and horizontal distances are the legs.
C. d = 3w − 1
Incorrect. You added the horizontal and vertical distance. To get the distance from one point to the other point, use the distance formula.
D. d = w − 5
Incorrect. You subtracted the horizontal and vertical distance. To get the distance from one point to the other point, use the distance formula.
A. 234 m
Incorrect. To solve for d, square both sides first.
B. 2296 m
Correct! This is the depth of the tidal wave.
C. 220,500 m
Incorrect. In the 2nd step, you multiplied by 9.8 to isolate the unknown. The inverse operation for multiplication is division.
D. 153 m
Incorrect. You forgot to square both sides first.
A. p = 4
Correct! This is the correct solution.
B. p = -4
Incorrect. If you used the algebraic method, you may have calculated a wrong sign. Check this answer using the graphing method.
C. p = 4.9 or p = -4.9
Incorrect. If you used the graphing method, you may have ignored the variable on the right.
D. No solution
Incorrect. If you solved algebraically, you simplified (p − 3)^2 incorrectly.
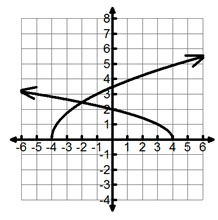
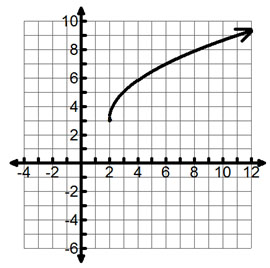
Based on this graph, which of the following is the solution?
A. {-4}
Incorrect. The x-intercept is the solution only when the equation is equal to 0.
B. {2}
Incorrect. The y-intercept is not the solution. Think about what the two graphs have in common.
C. {4}
Incorrect. The x-intercept is the solution only when the equation is equal to 0.
D. {-2}
Correct! The x-value of the intersection represents the intersection.

A
Incorrect. This formula requires that you subtract 9 and 8.5 first which will give the wrong cross-sectional surface area.
B
Correct! This formula will find the difference between the two terminal velocities.
C
Incorrect. This formula has the cross-sectional surface area and the weight reversed.
D
Incorrect. This formula subtracts the two weights and the two cross-sectional surface areas. Think about what the question is asking.
A. (2, -3)
Incorrect. This point is equal to a point on the boundary.
B. (8, -5)
Incorrect. This point is less than a point on the boundary.
C. (10, -4)
Correct! This point is greater than a point on the boundary.
D. (13, -7)
Incorrect. This point is less than a point on the boundary.
The formula to find the distance between two points is d = √(x2 − x1)2 + (y2 − y1)2 where d is the distance between (x1,y1) and (x2,y2). If the distance between (x1, -3) and (7,5) is 2√17, what is x1?
A. x1 = 9 or x1 = 5
Correct! Either of these x-values will yield a distance of 2 times the square root of 17.
B. No solution
Incorrect. If you used the algebraic method, you may have subtracted the y-values incorrectly.
C. x1 = 18.4
Incorrect. If you used the graphing method or the table method, you may have subtracted the two squares.
D. x1 = 7
Incorrect. If used the graphing method, you may have found the minimum point.
T = 2π√L/g
On a particular planet, the period of a pendulum is 1.5 seconds when the length of the pendulum is 0.6 meters. What is the acceleration due to gravity on this planet?
A. 4 m/sec2
Incorrect. If you solved algebraically, you may have substituted the period for the gravitational constant, g.
B. 10.5 m/sec2
Correct! This is the gravity constant.
C. 6.3 m/sec2
Incorrect. If you solved algebraically, you should eliminate the radical before you eliminate numbers under the radical sign.
D. 0.1 m/sec2
Incorrect. If you solved algebraically, examine your last step. Dividing by 6 does not isolate the variable.
Use the table method or the graphing method to solve √x + 5 > 3.
A. (- ∞, 4)
Incorrect. Looking at the table, you will see that these values are less than 3.
B. (-5, ∞)
Incorrect. If you used the graphing method, then you are looking at the x-intercept. You want the x-values where y is greater than 4.
C. (2.2, ∞)
Incorrect. If you are using the graphing method, you are looking at the y-intercept. You want the x-values where y is greater than 4.
D. (4, ∞)
Correct! Looking at the table, all the y-values after x = 4 are greater than 3.
Police use the formula s= √30fd to determine the speed of a car at an accident scene, where s is the speed in mi/h, d is length of the skid mark in feet, and f is drag factor (a measurement of the road friction). If the police determined that a car was traveling approximately 84.9 mi/hr and had a skid mark 32 feet in length, what drag factor was used to determine this speed?
A. 7.5
Correct! This is the drag factor that police used.
B. 0.1
Incorrect. You forgot to square the speed.
C. 7688.5
Incorrect. You should multiply 30 and 32 before dividing.
D. 6757.5
Incorrect. You should multiply 30 and 32 before dividing.
Given the quadratic f(x) = 2x2 − 5, which of the following is not a true statement about this function and its inverse?
A. The graph of its inverse reflects over the line y = x.
Incorrect. This is true.
B. Switching the x- and y- coordinates of f(x) to (y,x) produces the inverse.
Incorrect. This is true.
C. The equation for the inverse of f(x) is f -1(x) = √(1/2)x + 5.
Correct! This is false.
D. Its' inverse is not a function.
Incorrect. This is true.
Use the table method or the graphing method on your calculator to solve
√3 − 2x = √x + 8.
A. x = -1.7 or x = 2.5
Incorrect. You were correct that this is the intersection. Now think about which coordinate represents the solution.
B. No solution
Incorrect. If you are using the table method, you may not immediately see the intersection. Try changing the interval. Or look at the graph.
C. x = -1.7
Correct! This number will make each side equivalent to the other side.
D. x = 1.7
Incorrect. This is the x-intercept for one of the inequalities. You are looking for the intersection of the two inequalities.
Which of the following is the solution set for 3√2x - 5 = 15?
A. {10}
Incorrect. If you used the algebraic method, you forgot to square both sides.
B. {15}
Correct! This is the solution.
C. {74.5}
Incorrect. You may have subtracted 3 in step 1. Notice that the square root of 2x − 5 is being multiplied by 3.
D. No solution
Incorrect. You may have square the binomial 2x − 5 before eliminating the radical.