A.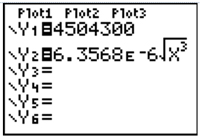
B.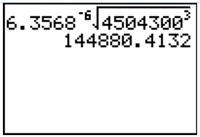
C.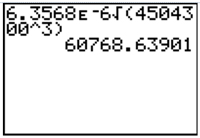
D.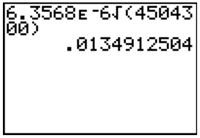
The astronomer Johannes Kepler (1571-1630) developed three laws of planetary motion that are still used. Kepler's Third Law states that the period of orbit T (in days) around the Sun for each planet can be modeled by the formula T = 6.3568 × 10-6 √d3, where d is the average distance (in kilometers) from the Sun. Neptune has an average distance of 4,504,300 km from the Sun. Which calculator screenshot below shows how to solve the number of days it takes Neptune to orbit the Sun?
|
A. |
B. |
|
|
C. |
D. |
A
Incorrect. Match the correct values and variables.
B
Incorrect. Enter the coefficient in scientific notation correctly.
C
Correct! You substituted the values given in the problem correctly in the equation.
D
Incorrect. According to the equation, it's the square root of the distance cubed.
Which graph below is the solution to the equation √x + 1 = x − 4
|
A. |
B. |
|
|
C. |
D. |
A
Correct! The left side of the equation is the square root function shifted 1 unit left, and the right side of the equation is the line with y-intercept -4 and slope of 1. The x-coordinate of the intersection of these two curves is the solution to the equation: x = 6.791.
B
Incorrect. The square root equation should be shifted 1 unit left.
C
Incorrect. Check the y = x − 4 graph.
D
Incorrect. Check the original equation again.
When a hockey player strikes a puck with a certain force, the velocity t seconds after striking the puck can be found by the equation v(t) = 27 − 9√t m/sec. Which table below shows the velocity of the puck at half-second intervals?
|
A. |
B. |
|
|
C. |
D. |
A
Incorrect. This shows the velocity at 2-second intervals.
B
Correct! You placed the values given and the variables correctly in the equation.
C
Incorrect. In this table, the velocities increase by .5 m/sec instead of 2 second intervals.
D
Incorrect. This is incorrect because at 1 second, the velocity would be v(1) = 27 − 9 multiplied by the square root of 1 = 18 m/sec.
Under certain conditions, a skydiver's terminal velocity, vt (in feet per second) is given by 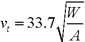 where W is the weight of the skydiver (in pounds) and A is the skydivers cross-sectional surface area (in square feet).
where W is the weight of the skydiver (in pounds) and A is the skydivers cross-sectional surface area (in square feet).
(Note that skydivers can vary their cross-sectional surface area by changing positions as they fall.)
What is the terminal velocity for a skydiver weighing 190 lbs. and with a cross-sectional area of 8 square feet?
A. 6.9 feet/sec
Incorrect. The weight and area values are switched.
B. 58.1 feet/sec
Incorrect. Take the square root of 190 divided by 8.
C. 4.9 feet/sec
Incorrect. Remember to multiply by 33.7.
D. 164.2 feet/sec
Correct! Good job substituting the values into the equation and evaluating it correctly.
At an accident scene, police measure the lengths of the skid marks to determine the initial speed of a vehicle before it started to brake. The formula used to determine the initial speed is S = √30f ∙ d, S is the speed (miles per hour), d is the average length of the skid marks in feet, and f is the drag factor, a measurement of the road friction. A car is traveling at 55 mph on dry asphalt with a drag factor of 0.8 slams on its brakes. What is the approximate length of the skid marks?
A. 36 feet
Incorrect. 55 is the speed of the car.
B. 158 feet
Incorrect. The 0.8 is under the radical.
C. 13 feet
Incorrect. 30 × 0.8 = 24.30
D. 126 feet
Correct! Nice job writing the equation and solving it for the distance!