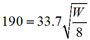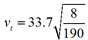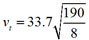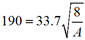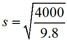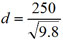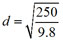Under certain conditions, a skydiver's terminal velocity, vt (in feet per second) is given by 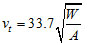 where W is the weight of the skydiver (in pounds) and A is the skydiver's cross-sectional surface area (in square feet). (Note that skydivers can vary their cross-sectional surface area by changing positions as they fall.) Select an appropriate equation for a skydiver weighing 190 lbs. with a cross-sectional area of 8 sq. ft.
where W is the weight of the skydiver (in pounds) and A is the skydiver's cross-sectional surface area (in square feet). (Note that skydivers can vary their cross-sectional surface area by changing positions as they fall.) Select an appropriate equation for a skydiver weighing 190 lbs. with a cross-sectional area of 8 sq. ft.
-
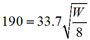
-
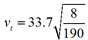
-
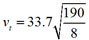
-
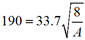
A
Incorrect. Put the values into the corresponding variables.
B
Incorrect. Put the values into the corresponding variables.
C
Correct! You put 190 and 8 in the right places.
D
Incorrect. Put the values into the corresponding variables.
A tsunami or tidal wave is a series of water waves caused by the displacement of a large volume of a body of water in an ocean or lake. The speed (in m/s) of a tsunami when moving in the deep ocean can be approximated by the square root of the product of g, the acceleration of gravity (9.8 m/s2), and the depth (in m) of the wave. What equation would give the speed of a 4000 m deep tsunami traveling across the Pacific Ocean?
- 9.8√4000
- √9.8(4000)
- √9.8 + 4000
-
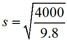
A
Incorrect. The speed is equal to the square root of the product of g and d.
B
Correct! You wrote the correct formula.
C
Incorrect. The speed is equal to the square root of the product of g and d.
D
Incorrect. The speed is equal to the square root of the product of g and d.
A tsunami or tidal wave is a series of water waves caused by the displacement of a large volume of a body of water in an ocean or lake. The speed (in m/s) of a tsunami when moving in the deep ocean can be approximated by the square root of the product of g, the acceleration of gravity (9.8 m/s2), and the depth (in m) of the wave. A tsunami's speed can be found using the formula s = √gd, where g = 9.8 m/s2. Scientists state that some tsunamis can travel as fast as a jet. If a Boeing 767 has a maximum cruising speed of 900 km/h (250 m/s), what equation would determine the depth of a tsunami with that same speed?
-
250 = √9.8d
- d = √9.8(250)
-
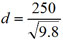
-
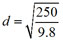
A
Correct! You placed 9.8 and 250 in the right places.
B
Incorrect. 250 is the speed.
C
Incorrect. This is not properly solved for d. Try again.
D
Incorrect. This is not properly solved for d. Try again.
The speed (in m/s) of a tsunami when moving in the deep ocean can be approximated by the square root of the product of g, the acceleration of gravity, (9.8 m/s2), and the depth (in m) of the wave. A tsunami's speed can be found using the formula s = √gd, where g = 9.8 m/s2. If a tsunami is traveling across a bay and its depth is doubled, its speed is 50 m/s greater. What equation could be used to determine the depth of the tsunami?
- √9.8d = √9.8(2d) + 50
-
√9.8d = 2√9.8d − 50
-
2√9.8d = √9.8d + 50
- √9.8d = 2√9.8d − 50
A
Incorrect. When the depth is doubled, the speed increases. To keep the quantities on both sides of the equal sign the same, 50 is removed from the expression with the higher speed.
B
Incorrect. The depth is not doubled in this equation.
C
Incorrect. Reread the problem and try again.
D
Correct! The depth was doubled or 2d.
At an accident scene, police measure the lengths of the skid marks to determine the initial speed of the vehicle before it started to brake. The formula used to determine the initial speed is S = √30f•d, where S is the speed (miles per hour), d is the average length of the skid marks in feet, and f is the drag factor, a measurement of the road friction determined by using either a drag sled or an accelerometer. A car traveling 55 mph on dry asphalt with a drag factor of 0.8 slams on its brakes, what equation would determine the approximate length of its skid marks?
-
S = √30(0.8)(55)
- 55 = 0.8√30d
-
55 = √30(0.8)d
- 55 = √240d
A
Incorrect. 55 is the speed.
B
Incorrect. The 0.8 is under the radical.
C
Correct! You placed 55 and 0.8 in the correct places.
D
Incorrect. 30 × 0.8 = 24.
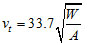 where W is the weight of the skydiver (in pounds) and A is the skydiver's cross-sectional surface area (in square feet). (Note that skydivers can vary their cross-sectional surface area by changing positions as they fall.) Select an appropriate equation for a skydiver weighing 190 lbs. with a cross-sectional area of 8 sq. ft.
where W is the weight of the skydiver (in pounds) and A is the skydiver's cross-sectional surface area (in square feet). (Note that skydivers can vary their cross-sectional surface area by changing positions as they fall.) Select an appropriate equation for a skydiver weighing 190 lbs. with a cross-sectional area of 8 sq. ft.