Solve the equation √4x − 7 = -3.

A. x = ½
Incorrect. You started off strong when solving the equation, but made a mistake along the way to the solution. Go back and check your work.

B. x = 1
Incorrect. Remember that to “undo” a square root, you must square sides of the equation. Go back and check your work.

C. x = 4
Incorrect. When you square the equation you should get -x = 4. (The radicand does not change when you square).

D. No solution
Correct! There is no value of x that will make this equation true.

Solve the equation 2√x − 5 + 11 = 15.

A. x = 7
Incorrect. 2√9 − 5 + 11 = 15 ⇒ 2√2 + 11 ≠ 15

B. x = 9
Correct! x = 9 makes the equation true.

C. x = 21
Incorrect. You started off strong when solving the equation, but made a mistake along the way to the solution. Go back and check your work.

D. x = 174
Incorrect. You made an algebra mistake along the way to the solution. Go back and check your work.

Solve the equation √3x + 16 = x + 2

A. x = 3
Correct! x = 3 makes the equation true.

B. x = -7
Incorrect. Remember that to “undo” a square root, you must square both sides of the equation. Go back and check your work.

C. x = -4 and 3
Incorrect. You solved the equation correctly, but only one of these answers makes the equation true. Remember that sometimes when you square an equation you can gain extraneous roots.

D. x = -3 and 4
Incorrect. You started off strong when solving the equation, but made a mistake when factoring or using the Quadratic Formula. Go back and check your work.

Solve the equation 4 √x  + 6 = 2 √x  + 18

A. x = -2
Correct! x = -2 makes the equation true.

B. x = 1
Incorrect. You did square to “undo” the square root and you remembered that the radicand remains the same. However, when the radicand comes out of the radical, it stays in parentheses. Did you distribute the coefficient?

C. x = 6
Incorrect. You did square to “undo” the square root and you remembered that the radicand remains the same. But when you square both sides, you must also square the coefficient of the radical. Go back and check your work.

D. No solution
Incorrect. While at first it appears that there isn’t a value that could make the radicands equal, you should still follow the steps to solve the equation.

The time T, in seconds, for a pendulum to complete one back-and-forth swing is given by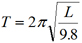
where L is the length of the pendulum in meters. What is the approximate length of a pendulum that completes one back-and-forth swing in 2.6 seconds?

A. 1.7 m
Correct! You substituted and solved correctly.

B. 40 m
Incorrect. Is this answer reasonable? Go back and check your calculations.

C. 62.9 m
Incorrect. Is this answer reasonable? Go back and check your calculations.

D. 163.5 m
Incorrect. Is this answer reasonable? Go back and check your calculations.