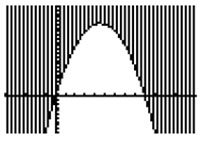
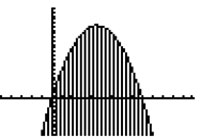
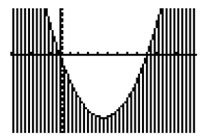
A dog owner has at most 24 feet of fencing with which to fence off a dog run. The possible areas of the run with this maximum perimeter can be modeled by the quadratic inequality A ≤ 9w - w² , where A is the area of the run and w is the width. Which graph below shows the possible widths and areas for this dog run?

A
Incorrect. The parabola opens downward and the shaded area is LESS than the values on the parabola.

B
Incorrect. The area is LESS than

C
Correct! The parabola opens downward and the area is LESS than the values on the parabola.

D
Incorrect. The parabola should open downward.

Given: x² + 7x + 10 ≤ 0. Which table below has the solution to the inequality shaded?

1. x	y
   -7	10
   -6	4
   -5	0
   -4	-2
   -3	-2
   -2	0
   -1	4

2. x	y
   -7	10
   -6	4
   -5	0
   -4	-2
   -3	-2
   -2	0
   -1	4

3. x	y
   -7	10
   -6	4
   -5	0
   -4	-2
   -3	-2
   -2	0
   -1	4

4. x	y
   -7	10
   -6	4
   -5	0
   -4	-2
   -3	-2
   -2	0
   -1	4

A
Correct! -5 ≤ x ≤ -2 yield y-values ≤ 0.

B
Incorrect. These yield y values > 0.

C
Incorrect. The solution set is x values.

D
Incorrect. The solution set is x values and these are not less than zero.

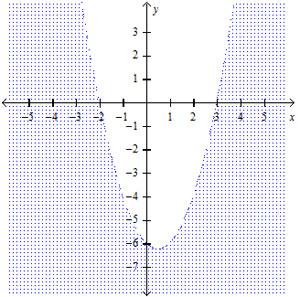
Which inequality is represented by this graph?

1. y > x ² − x − 6
2. y ≥ x ² − x − 6
3. y < x ² − x − 6
4. y ≤ x ² − x − 6

A
Incorrect. The shading is below the function, not above.

B
Incorrect. The graph would have a solid line and the shading would be below the function.

C
Correct! The parabola is dotted and the shading is below.

D
Incorrect. The parabola is dotted, not solid.

How many solutions does the inequality -x² − 8x − 16 ≥ 0 have?

A. No solutions.
Incorrect. The graph touches the x-axis and has one non-negative value.

B. One solution
Correct! The graph touches the x-axis at (-4,0) and, thus, has one value that is at least zero.

C. Two solutions
Incorrect. Quadratic inequalities have 0, 1, or infinite solutions.

D. Infinite solutions.
Incorrect. The graph has no values greater than zero - only one equal to zero.