What are the zeros of the function y = 2(x + 3)(x − 5)?

A. 3 and -5
Incorrect: This answer indicates the same values as the constant in each binomial instead of the zeros.

B. 2 and 3/5
Incorrect: You just picked an arrangement of the numbers instead of creating the zeros.

C. -3 and 5
Correct! Replacing x with these two values will create the zero factors needed.

D. -2 and -3/5
Incorrect: You just picked an arrangement of the numbers instead of creating the zeros.

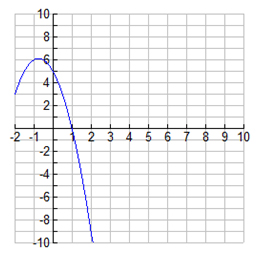
Part of the graph of a quadratic equation is shown below:

If the line of symmetry for this quadratic equation is x = -.75, between which two integers will the other part of the graph intersect the x-axis?

A. -4 and -3
Incorrect. 1.75 left of -.75 is not between -4 and -3.

B. -2 and -3
Correct! -2.5 is between -2 and -3 and 1.75 from the line of symmetry.

C. 0 and 2
Incorrect. The x = 1 intercept is between 0 and 2.

D. 2 and 3
Incorrect. These are the opposite points on the axis.

Given the following table of values for a quadratic function, which of the ordered pairs would be a zero for the function?

A. (2, 0)
Correct! It fits the pattern for this function.

B. (0, 2)
Incorrect. The point (0,0) is already a point on the graph, which means you cannot have another points with a x-value of 0.

C. (-4, 0)
Incorrect. As the domain gets smaller the range will get larger due to the pattern in the table.

D. (2.5, 0)
Incorrect. This does not fit the pattern in the quadratic table.

Using the quadratic formula,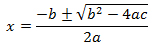

A. x = 4, -5
Incorrect. You forgot some sign rules on your values.

B. x = .725 , -1.725
Incorrect. You used 4 instead of ¼ for b and the formula gives you these values incorrectly.

C. x = 5, -4
Incorrect. Sign values got you these incorrect roots.

D. x = -10, 2
Correct! If you use the formula correctly these are your roots.

The height, h(t), in meters, of a falling object can be represented by the formula h(t)= -4.9t² + d, where d is the initial height, in meters, of the object above the ground, and t is the time, in seconds, the object has been falling. If an object is dropped from a height of 15 meters, how long does it take the object to hit the ground? Round the answer to the nearest hundredth of a second.

A. 1.75 seconds
Correct! To make this equation true, 0 = -4.9t + 15, t must equal 1.75.

B. 2.00 seconds
Incorrect. You rounded to the ones place instead of the hundredths place.

C. -1.75 seconds
Incorrect. Time cannot be measured negatively.

D. 10.1 seconds
Incorrect. Does that make sense to you to fall only 15 feet?