The table below represents the values of a quadratic equation in standard form.
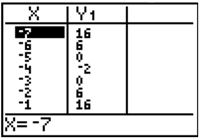
Based on this table, what is the solution(s) for this equation?
A
Incorrect. The solution of a quadratic equation is related to the x-intercept.
B
Correct! The solution to a quadratic equation is found when y = 0.
C
Incorrect. You are looking for the x-value when the value of the quadratic is 0.
D
Incorrect. Find the y1 value that represents the solution of the quadratic.
The table represents the values of a quadratic equation in standard form.
|
x
|
y
|
|
0
|
72
|
|
1
|
50
|
|
2
|
32
|
|
3
|
18
|
|
4
|
8
|
|
5
|
2
|
|
6
|
0
|
|
7
|
2
|
|
8
|
8
|
|
9
|
18
|
|
10
|
32
|
What does this table tell you about the solution(s)?
A. No solution
Incorrect. The solution of a quadratic equation is related to the x-intercept.
B. 1 solution
Correct! Only x=6 has a y –value of 0.
C. 2 solutions
Incorrect. Recall that the x-intercept(s) is the solution.
D. 3 solutions
Incorrect. Think about the maximum number of x-intercepts for a quadratic function.
The table represents the values of a quadratic equation in standard form.
|
x
|
y
|
|
-7
|
15
|
|
-6
|
2
|
|
-5
|
-7
|
|
-4
|
-12
|
|
-3
|
-13
|
|
-2
|
-10
|
|
-1
|
-3
|
|
0
|
8
|
|
1
|
23
|
|
2
|
42
|
Based on this table, the roots are between what x-values?
A. 2 and -7, -3 and 8
Incorrect. Find the corresponding x-values for these zeros.
B. -7 and -5, -1 and 1
Incorrect. Can you narrow down the solution?
C. -1, 1
Incorrect. First find where 0 might be located in the y-column.
D. -6 and -5 or -1 and 0
Correct! You noticed the change in the sign of the y-values.
The table below represents some of the values of a quadratic equation in standard form.
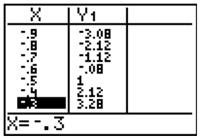
Which of the following would be the best approximation of the root described by this table?
A. -.6
Correct! -.08 is closest to 0.
B. -.3
Incorrect. First, find the y-value that is closest to 0.
C. -.08
Incorrect. Once you find the y-value closest to zero, locate the corresponding x-value.
D. -.5
Incorrect. There is another corresponding y-value closer to 0.