Any object influenced by gravity falls freely according to the equation: h(t) = -16t² + v₀t + h₀, where v₀ is initial velocity, and h₀ is the initial height above the ground. Assume a particular object has motion described by the quadratic function h(t) = -16t² + 100t + 4, with an initial velocity of 100 ft/s and an initial height of 4 ft above the ground. What is h(3), and what does it mean?

1. h(3) = 160; The object is 160 feet above the original launch height of 4 feet at t = 3 seconds.
2. h(3) = 160; The object is 160 feet above the ground at t = 3 seconds.
3. h(3) = 448; The object is 448 feet above the original launch height of 4 feet at t = 3 seconds.
4. h(3) = 448; The object is 448 feet above the ground at t = 3 seconds.

A
Incorrect. The value for h(3) shows the position of the object above the ground when t = 3 seconds.

B
Correct! h(3) = -16(3)² +100(3)+4, or h(3) = 160.

C
Incorrect. You forgot to use a negative when evaluating -16(3)².

D
Incorrect. You forgot to use a negative when evaluating -16(3)².

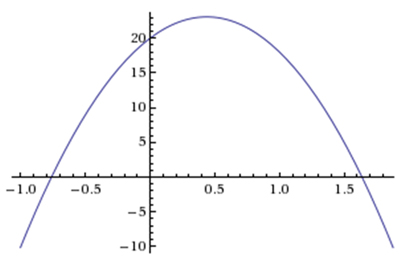
Any object influenced by gravity falls freely according to the equation: h(t) = -16t² + v₀t + h₀, where v₀ is initial velocity, and h₀ is the initial height above the ground. A spring loaded cannon launches a steel marble vertically according to the following quadratic function: h(t) = -16t² + 96t + 20, where 96 ft/s is the initial velocity and 20 feet is the initial height above the ground. How do you find the time when the marble is 100 feet in the air, and what is (are) the solution(s)?

1. Evaluate h(100) = -16(100)² + 96(100) + 20.
   t = -150,380 is the only solution.
2. Evaluate h(100) = -16(100)² + 96(100) + 20.
   t = -150,380 would be the only solution, but it is an extraneous solution; therefore, there is no solution.
3. Solve the equation: 100 = -16t² + 96t + 20.
   t = 5 is the only solution.
4. Solve the equation: 100 = -16t² + 96t + 20.
   t = 1 and t = 5 are both valid solutions.

A
Incorrect. Evaluating h(100) would find the vertical position at t = 100 seconds.

B
Incorrect. Evaluating h(100) would find the vertical position at t = 100 seconds.

C
Incorrect. There is no reason to exclude t =1 from the solution. Only negative times are excluded.

D
Correct! The marble is 100 feet above the ground on its way up at t =1, then reaches a height of 100 feet on its way back down at t = 5.

A physics student gently tosses a coin straight up at a speed of 14 ft/s from the edge of a building 20 feet in the air. A short time later the coin lands harmlessly on the ground below. The coin's vertical motion can be described by the quadratic function h(t)=-16t²+14t+20, where h is vertical height at any time t. The student graphs h(t) and finds intercepts at (0,20),(-0.76,0), and (1.64,0). Which statement is true?

A. The coin is in the air for 0.76 seconds.
Incorrect. The coin is in the air starting at t = 0 seconds until t = 1.6 seconds.

B. The coin is in the air for 1.64 seconds.
Correct! The root (1.64,0) implies the coin reaches the ground, or height h = 0, at approximately time t = 1.64.

C. The coin is in the air for 2.40 seconds.
Incorrect. Do not add the times together. Remember, you begin the experiment at t = 0.

D. The coin is in the air for 20.00 seconds.
Incorrect. The ordered pair (0,20) tells you the initial height is 20 ft.

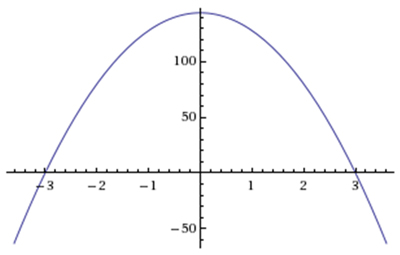
A physics student climbs to the top of a neighboring building and drops the coin from rest from the edge of a building 144 feet in the air. This coin’s vertical motion can be described by the quadratic function h(t)=-16t²+144, where h is vertical height at any time t. The student graphs h(t) and finds roots at (-3, 0), and (3, 0). Which of the following statements are true?

1. The coin is in the air for 3 seconds.
2. The coin is in the air for 6 seconds.
3. At time t = 3, the coin is at position h = 0 (on the ground).
4. At time t = 2, the coin is 80 feet in the air.

A. II only
Incorrect. Do not add the times together. Remember, you begin the experiment at t = 0.

B. II and IV only
Incorrect. Do not add the times together. Remember, you begin the experiment at t = 0. There are other true statements. Try again.

C. I and III only
Incorrect. There is another true statement.

D. I, III and IV only
Correct! Since the coin is in the air for 3 seconds, it will land on the ground at t = 3. Also, by evaluating h(2) = -16(2)² +144, you find h(2) = 80, meaning the coin is 80 feet in the air at t = 2 seconds.