A quadratic function has zeros at -2 and 3 and its graph has a maximum point. Which graph below best represents this function?

A. B.
C. D.

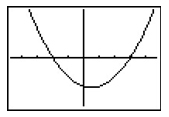
A
Incorrect. This graph has a minimum not a maximum.

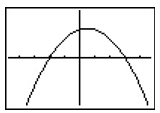
B
Correct!! The graph crosses the x-axis at (-2,0) and (3, 0) and opens downward, thus having one maximum point at its vertex.

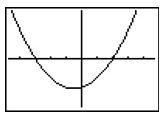
C
Incorrect. This graph has a minimum not a maximum and roots are -3 and 2.

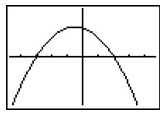
D
Incorrect. The roots here are -3 and 2.

A homeowner uses 800 feet of fencing to enclose a dog run in his back yard. Write an equation expressing the area, A, of the rectangular dog run as a function of w, the width of the rectangle.

A. -w2 + 800w = A
Incorrect. You must have thought that the length of the rectangle could be represented by 800 − w. The length should be 400 − w because of the relationship of the length, width, and perimeter of a rectangle.

B. w2 − 400w = A
Incorrect. This one will give you a negative value for the length and a minimum area instead of a maximum area (hint: the parabola must open downward).

C. -w2 + 400w = A
Correct! If the width is “w”, then the length must be “400 − w,” so the area is the product w(400 − w).

D. -2w2 + 400w = A
Incorrect. You must have thought that the length of the rectangle could be represented by 400 − 2w. The length should be 400 − w because of the relationship of the length, width, and perimeter of a rectangle.

Which quadratic function has a minimum but no real zeros?

  1. y = 2x2 + 3x − 6
    Incorrect. This parabola has a vertex in the 3rd Quadrant and opens upward. Therefore, it does cross the x-axis and has two real zeros.
  2. y = -2x2 − 3x + 6
    Incorrect. This parabola has its vertex in the 1st Quadrant and opens downward. Therefore, it crosses the x-axis and has two real roots.
  3. y = 2x2 − 3x + 6
    Correct! This parabola has its vertex in the 1st Quadrant and opens upward. Therefore, it never intersects the x-axis and has no real zeros.
  4. y = -2x2 + 3x + 6
    Incorrect. This parabola has its vertex in the 1st Quadrant and opens downward. Therefore, it crosses the x-axis and has two real roots.

Cory described a quadratic function as one that has two real zeros and a maximum. Which table of values best represents Cory’s function?

A.
x
-1
0
1
2
3
y
0
3
4
3
0
B.
x
-1
0
1
2
3
y
12
7
4
3
4
C.
x
-1
0
1
2
3
y
-12
-7
-4
-3
-4
D.
x
-1
0
1
2
3
y
4
-1
-4
-5
-4

A
Correct! The two real zeros (or x-intercepts) occur at (-1, 0) and (3, 0) and the maximum (vertex) occurs at (1, 4) with y-values less in both directions.

B
Incorrect. By looking at the y-values, you can see that all the points on this parabola are above the x-axis--no real zeros. Also, instead of a maximum, this parabola has a minimum.

C
Incorrect. Looking at the y-values, you can see that all the points on this parabola are below the x-axis--no real zeros. Also, this parabola opens downward and has a maximum, but the maximum is below the x-axis.

D
Incorrect. This parabola crosses the x-axis, so has real zeros, but has a minimum at (2, -5), not a maximum.

Which of the following equations is that of a quadratic function with a minimum in the 4th Quadrant and two real zeros?

  1. y = -(x − 2)(x − 3) − 5
    Incorrect. This one has a maximum.
  2. y = (x − 2)(x + 3) − 5
    Incorrect. This one’s vertex is not where described.
  3. y = (x − 2)(x − 3) − 5
    Correct! The vertex (2.5, -5.25) has been translated to the right and down from the origin and the parabola opens upward, crossing the x-axis at two points.
  4. y = (x + 2)(x + 3) − 5
    Incorrect. The parabola has been moved the wrong direction for its minimum to be in the 4th Quadrant.