Which statement correctly describes the effect on the graph of f(x) = one over the quantity (x minus 1) 1 (x − 1) + 3 when it is changed to f(x) = four over the quantity (x minus 1) 4 (x − 1) − 2 ?
A. The graph is vertically stretched and is shifted to the left.
Incorrect. You are correct in that it is vertically stretched but notice the negative “k” value.
B. The graph is vertically stretched and is shifted down.
Correct! Yes, the 4 makes the graph stretch and the -2 shifts the graph down.
C. The graph is vertically compressed and is shifted down.
Incorrect. You are correct in that it shifts down but notice the increase in the “a” value.
D. The graph is vertically compressed and is shifted to the right.
Incorrect. Notice the increase in the “a” value as well as the negative “k” value.
Which statement correctly describes the effect on the graph of f(x) = one over the quantity (x minus 5) 1 (x − 5) − 3 when it is changed to f(x) = 1 over the quantity (x plus 2) 1 (x + 2) − 3 ?
A. The graph is translated 7 units to left.
Correct! Subtracting the “h” values of 5 and -2 gives you an “h” value of 7 so that’s a left shift.
B. The graph is translated 7 units to right.
Incorrect. You need to subtract the h values and notice its sign.
C. The graph is translated 7 units up.
Incorrect. The “k” values determine a shift up or down. In this problem, the “k” value stayed the same.
D. The graph is translated 7 units down.
Incorrect. The “k” values determine a shift up or down. In this problem, the “k” value stayed the same.
Which statement correctly describes the the transformation of the parent function f(x) = one over x 1 x to the rational function graphed below?
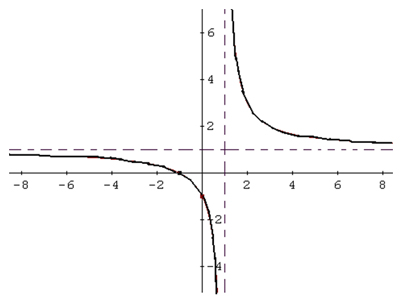
A. The graph is translated 1 unit to the left and 1 unit down.
Incorrect. The parent function has a horizontal asymptote at y = 0 and a vertical asymptote at x = 0. Notice how the asymptotes in the graph move from those of the parent function.
B. The graph is translated 1 unit to the right and 2 units up.
Incorrect. You are correct in that it is translated 1 unit to the right but look at the horizontal asymptote compared to the parent function’s horizontal asymptote at y = 0.
C. The graph is translated 1 unit to the right and 1 unit up.
Correct! You noticed that the vertical asymptote move 1 unit to the right of x equals 0 and 1 unit up from y = 0.
D. The graph is translated 1 unit to the left and 2 units down.
Incorrect. The parent function has a horizontal asymptote at y = 0 and a vertical asymptote at x = 0. Notice how the asymptotes in the graph move from those of the parent function.
The rational parent function is translated 3 units to the right and 6 units up. What is the equation of the new graph?
A
Incorrect. Check the “h” value again.
B
Correct! The “h” value is 3 and the “k” value is 6.
C
Incorrect. You switched the “h” and “k” values.
D
Incorrect. You switched the “h” and “k” values as well as the signs.
Which of the following functions is a transformation of f(x) = one over x 1 x , where the new rational function has been vertically stretched, shifted to the left, and shifted down?
A
Incorrect. The negative “a” value reflects the graph, not stretch it.
B
Incorrect. Look at the “a” value. It is between 0 and 1 and therefor will compress the graph.
C
Incorrect. Look at the “h” and “k” value again.
D
Correct! The “a” value is greater than 1, “h” is positive, and “k” is negative.
You have been given a table of values for the function f(x) = two over x 2 x + 3
| X | Y |
|---|---|
| -2 | 2 |
| -1 | 1 |
| 0 | Undefined |
| 1 | 5 |
| 2 | 4 |
If the graph of this function is translated down 4 units, which of the tables shown below would be points on the new graph?
| X | Y |
|---|---|
| -6 | 2 |
| -5 | 1 |
| -4 | Undefined |
| -3 | 5 |
| -2 | 4 |
| X | Y |
|---|---|
| -2 | -2 |
| -1 | -3 |
| 0 | Undefined |
| 1 | 1 |
| 2 | 0 |
| X | Y |
|---|---|
| -2 | 6 |
| -1 | 5 |
| 0 | Undefined |
| 1 | 9 |
| 2 | 8 |
| X | Y |
|---|---|
| -2 | 2 two-thirds23 |
| -1 | 2 three-fifths35 |
| 0 | Undefined |
| 1 | 2 one-third13 |
| 2 | 2 |
A
Incorrect. You translated the x values when you should have changed the y values.
B
Correct! You correctly subtracted 4 from the y values in order to shift the graph down.
C
Incorrect. You shifted the graph up instead of down.
D
Incorrect. Remember, to shift up and down you must change the “k” value.