Which statement correctly describes the graph of y = - 6 | x + 2 | + 5?

  1. It is narrower than the graph of y = | x | translated 2 units to the left and 5 units up.
  2. It is wider than the graph of y = | x |, reflected across the x-axis, then translated 2 units to the right and 5 units down.
  3. It is the graph of y = | x |, reflected across the x-axis, then translated 2 units to the left and 5 units up.
  4. It is narrower than the graph of y = | x |, reflected across the x-axis, then translated 2 units to the left and 5 units up.

A
Incorrect. Did you notice that “a” is negative?

B
Incorrect. For the graph to be wider than y = | x |, | a | < 1.

C
Incorrect. Did you notice that the | a | > 1?

D
Correct! Since “a” is negative and a > 1, the graph opens down and is narrower.

The graph of f(x) = - 5 | x – 1 | + 5 is translated 3 units to the right. What is the equation of the new graph?

A. f(x) = -5 | x – 4 | + 5
Correct! For a horizontal shift to the right, you should add 3 to “h” in the equation f(x) = a | x – h | + k.

B. f(x) = -5 | x + 2 | + 5
Incorrect. For a horizontal shift to the right, you should add 3 to “h” in the equation f(x) = a | x – h | + k

C. f(x) = -5 | x – 1 | + 8
Incorrect. Remember that a horizontal translation affects the “h” in the equation f(x) = a | x – h | + k

D. f(x) = -7 | x – 1 | + 5
Incorrect. Remember that a horizontal translation affects the “h” in the equation f(x) = a | x – h | + k

Which of the following functions is a transformation of y = | x |, where the new graph is wider and has been translated to the left?

A. y = ? | x – 7 |
Incorrect. This one is wider than y = | x |, but is translated to the right instead of to the left.

B. y = ½ | x | - 6
Incorrect. This one is wider than y = | x |, but is translated down instead of to the left.

C. y = 4 | x + 5 |
Incorrect. This one is translated to the left, but is narrower than y = | x |

D. y = ¾ | x + 3 |
Correct! This one is wider than y = | x | because |a| decreases from 1 to ¾. It moves to the left because “h” decreases from 0 to -3.

You have been given a table of values for an absolute value function.

x
y
-2
7
-1
5
0
3
1
1

If the graph of this function is translated 4 units down, which of the tables shown below would be points on the new parabola?

A.
x
y
-2
11
-1
9
0
7
1
5
C.
x
y
-2
3
-1
1
0
-1
1
-3
B.
x
y
-6
7
-5
5
-4
3
-3
1
D.
x
y
-6
3
-5
1
-4
-1
-3
-3

A
Incorrect. To shift down, you should SUBTRACT from each of the y-values.

B
Incorrect. When you shift vertically, it should affect only the y-values.

C
Correct! To shift down, you should subtract from each of the y-values.

D
Incorrect. When you shift vertically, it should affect only the y-values.

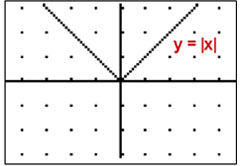
The graph of y = | x | is shown on the graph below.

Which of the following best represents the graph of y = -2 | x – 1 | ?

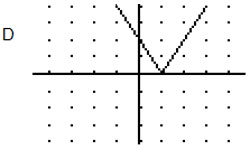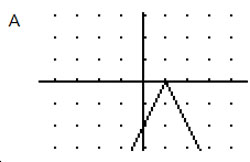
A
Correct! The absolute value graph is reflected across the x-axis and narrower than the parent graph because “a” is negative and |a| > 1. Since h = 1, it has been shifted 1 unit to the right.

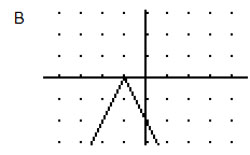
B
Incorrect. The vertex form of this absolute value graph is y = -2 | x – 1 |. In this equation h= 1. How is the graph affected if “h” is positive?

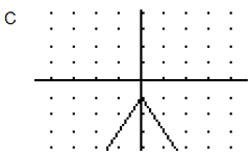
C
Incorrect. The vertex form of this absolute value graph is y = -2 | x – 1 |. In this equation h= 1. Remember that “h” affects ONLY horizontal movement.

D
Incorrect. The vertex form of this absolute value graph is y = -2 | x – 1 |. In this equation a = -2. How is the graph affected if “a” is negative?