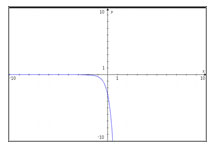
Incorrect. This graph is a reflection through the x-axis, so function values have been multiplied by -1.
If the exponential function f(x) = 10x is transformed to g(x) = 10x + 4, what will happen to the graph of the function?
A. The graph will stretch horizontally.
Incorrect. The change from f(x) to g(x) is the addition of 4, which creates a vertical shift up.
B. The graph will narrow horizontally.
Incorrect. The change from f(x) to g(x) is the addition of 4, which creates a vertical shift up.
C. The graph will move up 4 units.
Correct! Yes, the change from f(x) to g(x) is the addition of 4, which creates a vertical shift up of 4.
D. The graph will move down 4 units.
Incorrect. You are correct that the graph did move vertically, but the change from f(x) to g(x) is the addition of 4, which creates a vertical shift up.
This is the exponential graph of f(x) = 10x.
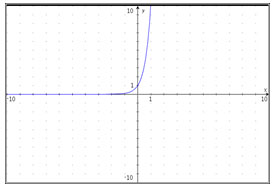
If the graph is transformed to g(x) = 3(10x) which of the following is the new graph?
A.

Incorrect. This graph is a reflection through the x-axis, so function values have been multiplied by -1.
B.
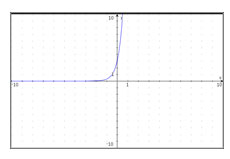
Correct! All the function values of the graph have been multiplied by 3, so (0, 1) becomes (0, 3).
C.

Incorrect. This graph moved up 4 units, so 4 was added to the function.
D.
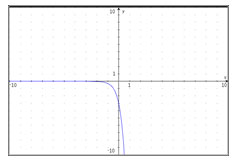
Incorrect. This graph has been multiplied by -3, not positive 3.
What is the difference between the graphs of these two exponential functions?
f(x) = 10x
g(x) = 10(x − 3)
A. The graph of g(x) is 3 units to the right of the graph of f(x).
Correct! The exponent changed to x – 3, so the graph moved right.
B. The graph of g(x) is 3 units to the left of the graph of f(x).
Incorrect. The exponent would have to be x + 3 to move the graph left.
C. The graph of g(x) is 3 units above the graph of f(x).
Incorrect. For the graph to move up, the equation would have to be changed to g(x) = 10x + 3.
D. The graph of g(x) is 3 units below the graph of f(x).
Incorrect. For the graph to move down, the equation would have to be changed to g(x) = 10x – 3.
Which of the following functions is a transformation of f(x) = log(x), where the new logarithmic function has been vertically stretched, shifted to the left, and shifted down?
A. f(x) = 1 3 log(x + 6) – 9
Incorrect. The function has been multiplied by 1 3 , which would create a vertical compression.
B. f(x) = 3log(x + 8) – 6
Correct! The 3 creates a vertical stretch, the -8 moves the graph to the left, and the 6 creates a vertical shift down.
C. f(x) = 4log(x + 7) + 3
Incorrect. The 3 would move the graph up instead of down.
D. f(x) = 1 5 log(x) – 2
Incorrect. The 1 5 would create a vertical compression and the -2 would shift the graph down.
Which statement correctly describes the transformation of the parent function, f(x) = log(x), to the logarithmic function graphed below?
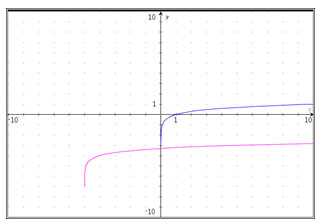
A. The parent function is translated 5 units to the left and 4 units down.
Correct!
B. The parent function is translated 4 units up and 5 units to the right.
Incorrect. Identify where the vertical asymptote moves, and then use a point on the graph to follow the translation to the new function.
C. The graph is reflected across the x-axis.
Incorrect. This is a horizontal and vertical shift from the parent function.
D. The graph is translated 5 units to the right and 4 units down.
Incorrect. You are correct in that the graph shifted down 4 units, but look again at the horizontal shift. Use the vertical asymptote to help you locate the horizontal shift.