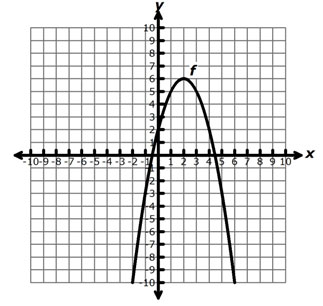
The graph of a quadratic function, f, is shown on the grid below.

If the graph of f is translated 4 units to the left and 8 units down to create a new graph, which function best represents this new graph?

A. g(x) = -(x – 4)² – 8
Incorrect. These constants, h and k represent the transformation, not the equation of the resulting graph.

B. g(x) = -(x + 2)² + 6
Incorrect. This function represents the original function, f.

C. g(x) = -(x + 2)² – 2
Correct!

D. g(x) = -(x + 6)² – 2
Incorrect. This function represents a horizontal shift of 4 units to the right, instead of 4 units to the left.

The graph of a quadratic function, f, is shown on the grid below.

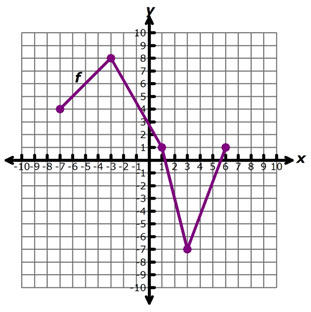
If the graph were translated 3 units to the right and 2 units down, what would be the new x-values be for the points that are indicated on the graph?

A. {x: x ∈ -7, -3, 1, 3, 6}
Incorrect. This is the domain of the original function, f.

B. {x: x ∈ -4, 0, 4, 7, 9}
Correct!

C. {x: x ∈ -10, -6, -2, 0, 3}
Incorrect. This is the domain of a function that is translated 3 units to the left.

D. {x: x ∈ -7, 1, 4, 8}
Incorrect. This is the domain of the original function, f.

The parent function, f(x) = 2^x, and the transformed function g(x) are both shown in the graph below.

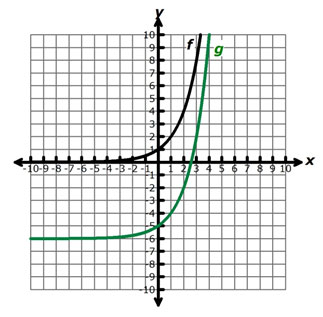
If g(x) is a vertical translation of f(x), which of the following best represents g(x)?

A. g(x) = 2^x – 6
Correct!

B. g(x) = 2^x + 6
Incorrect. This function represents a vertical translation up 6 units from the parent function.

C. g(x) = 2^{x – 6}
Incorrect. This function represents a horizontal translation right 6 units from the parent function.

D. g(x) = 2^{x + 6}
Incorrect. This function represents a horizontal translation left 6 units from the parent function.

The parent function, f(x) = 1 x , has been transformed to generate the graph of the function g(x), as shown in the figure below.

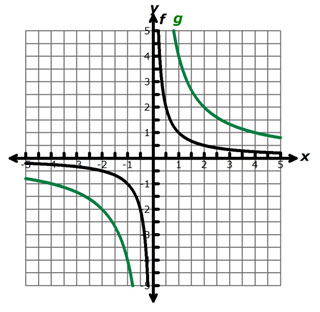
Which of the following best represents g(x)?

A. g(x) = 1 x + 4
Incorrect. This function represents a vertical translation, and that is not the transformation shown in the graph.

B. g(x) = 1 x – 4
Incorrect. This function represents a horizontal translation, and that is not the transformation shown in the graph.

C. g(x) = 1 4x
Incorrect. How does the y-coordinate of the point (1, 1) change from the graph of the parent function to the graph of the transformed function?

D. g(x) = 4 x
Correct!

The parent function f(x) = √x is transformed to generate the function g(x) = - √x – 4. Which of the following best describes that transformations that were used to generate g(x) from f(x)?

A. The parent function is translated 4 units to the right and reflected across the line y = 0.
Correct!

B. The parent function is translated 4 units to the right and reflected across the line x = 0.
Incorrect. The negative sign in front of the radical indicates a reflection across a horizontal line, and x = 0 is a vertical line (the y-axis).

C. The parent function is translated 4 units to the left and reflected across the line y = 0.
Incorrect. A horizontal translation is in the opposite direction from the sign present in the function.

D. The parent function is translated 4 units to the left and reflected across the line x = 0.
Incorrect. Since the negative sign appears in front of the radical, there is a reflection across a horizontal line. Also, a horizontal translation is in the opposite direction from the sign present in the function.