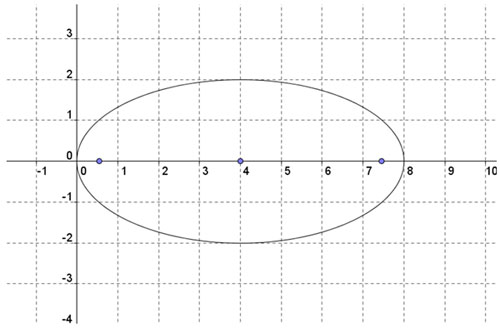
Which of the following is the equation of the ellipse shown in the graph?

A. (x + 4)2 16 + y2 4 = 1
Incorrect. Check the values of h and k for location of the center.

B. (x − 4)2 16 + y2 4 = 1
Correct! Center (4, 0) with major or x-radius = 4 units and minor or y-radius = 2 units.

C. (x − 4)2 4 + y2 2 = 1
Incorrect. Check the x-radius and y-radius.

D. (x + 4)2 4 + y2 2 = 1
Incorrect. Check the x-radius and y-radius

Which of the following is the equation of an ellipse with center (-2, 3) and with major or x-radius length 5 units and minor or y-radius length 6 units?

A. (x + 2)2 10 + (y − 3)2 12 = 1
Incorrect. Center is correct, but x- and y-radii must be the square roots of the numbers in the equation.

B. (x + 2)2 25 + (y − 3)2 36 = 1
Correct!

C. (x + 2)2 36 + (y − 3)2 36 = 1
Incorrect. check the major and minor radius values.

D. (x + 3)2 25 + (y − 2)2 36 = 1
Incorrect. The center of this ellipse will be (-3, 2).

If an ellipse has its center at the origin, x-radius 7 units, y-radius 5 units, which of the following ordered pairs could be those of the two foci of the ellipse?

A. (-24, 0) (24, 0)
Incorrect. Take the square root.

B. (0, -24) (0, 24)
Incorrect. Take the square root; foci must be on the x-axis.

C. (-4,89, 0) (4.89, 0)
Correct!

D. (0, -4.89) (0, 4,89)
Incorrect. Foci must be on x-axis.

Which is the graph of this ellipse? x2 49 + (y + 2)2 9
A.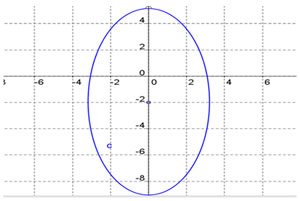 B.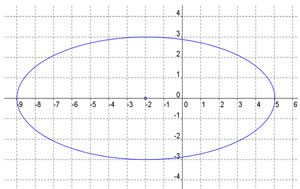
C.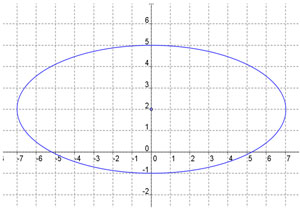 D.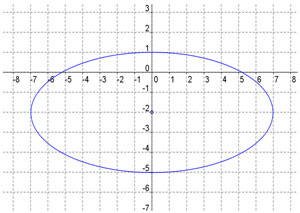

A
Incorrect. Check the x-radius and the y-radius.

B
Incorrect. Check the coordinates of the center.

C
Incorrect. Check the coordinates of the center.

D
Correct! Center (0, -2) x-radius = 7, y-radius = 3

Which of the following best describes the differences in the graphs of the following two ellipses.

  1. (x + 4)2 25 + (y − 1)2 64 = 1
  2. (x − 4)2 64 + (y + 1)2 25

A. Ellipse I has center (-4, 1) and a vertical major axis. Ellipse II has center (4, -1), horizontal major axis.
Correct! Ellipse I: h = -4, k = 1, y-radius is longer, so major axis in “y” direction-vertical and ellipse II: h = 4, k = -1, x-radius is longer, so major axis if in “x” direction-horizontal.

B. Ellipse I has center (4, -1), x-radius 5 units, y-radius 8 units, and a horizontal major axis. Ellipse II has center (-4, 1), x-radius 5 units, y-radius 8 units; vertical major axis.
Incorrect. Center coordinates for the two ellipses are reversed. Ellipse I should be in Quadrant II and Ellipse II should be in Quadrant IV, not the other way around.

C. Ellipse I has center (-4, 1) in Quadrant II and a horizontal major axis. Ellipse II has center (4, -1) in Quadrant IV and a vertical major axis.
Incorrect. Check the lengths of the two axes to determine the direction of the major axes.

D. Ellipse II is Ellipse I translated 8 units to the right and 2 units down.
Incorrect. Ellipse II has a horizontal major axis while Ellipse I has a vertical major axis.