Which of the following is the equation of the circle graphed?

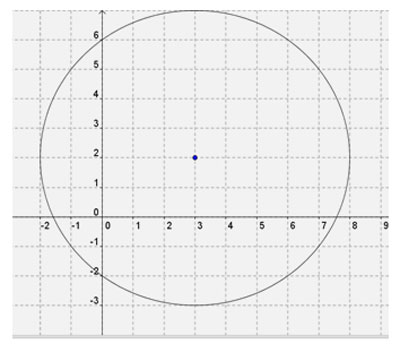
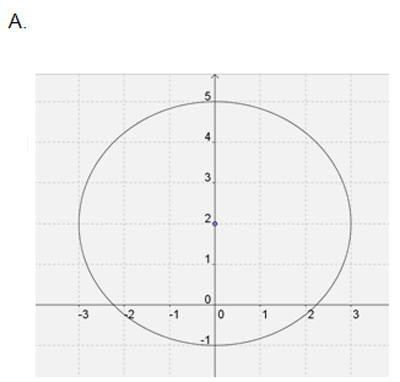
A. x2 + 6x + y2 + 2y − 25 = 0
 
B. x2 + 6x + y2 + 2y = -25
 
C. (x − 3)2 + (y - 2)2 = 25
 
D. (x − 2)2 + (y − 3)2 = 25

A
Incorrect. When squares are completed, the center will be (-3, -2), not (3, 2)

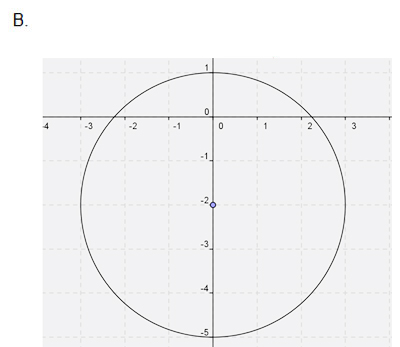
B
Incorrect. When squares are completed, the center will be (-3, -2) and the radius will be negative. Impossible!

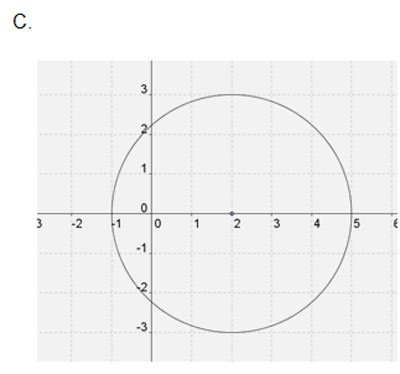
C
Correct! Center at (3, 2) and radius square root of 25 = 5.

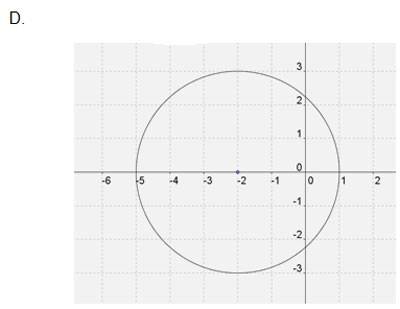
D
Incorrect. “h” and “k” reversed. Center (2, 3).

Which of the following is the equation of a circle with center at (- 4, 3) and radius 6 units?

A. (x - 4)2 + (y + 3)2 - 36 = 0
 
B. (x + 4)2 + (y - 3)2 - 36 = 0
 
C. (x + 4)2 + (y - 3)2 + 36 = 0
 
D. (x - 3)2 + (y + 4)2 − 36 = 0

A
Incorrect. Center (4, -3), radius 6 units

B
Correct! Center (-4, 3), radius 6 units

C
Incorrect. Center (-4, 3), radius negative.

D
Incorrect. Center (3, -4), radius 6 units.

Which is the graph of this circle: x2 + (y + 2)2 = 9?

 
     
 

A
Incorrect. h=0, k=2, r=3 Center (0,2)

B
Correct! h = 0, k = -2, r = 3, so center (0, -2)

C
Incorrect. h=2, k=0, Center (2,0)

D
Incorrect. h=-2, k=0, Center (-2,0)

How would the following two circles differ when graphed?

  1. (x − 2)2 + y2 = 16
  2. x2 + (y − 2)2 = 16

A. Circle I has center at (-2, 0) and circle II has center at (2, 0). Both have radius 4 units.
Incorrect. h = 2, not -2 in Circle I and h = 0 with k = 2 in Circle II.

B. Circle I has center at (2, 0) and circle II has center at (0, 2). Both have radius 4 units.
Incorrect: h = 0 and k = 2 in Circle—center at (0, 2). r2 = 16, so radius is 4 units.

C. Circle I has center at (-2, 0) and circle II has center at (2, 0). Both have radius 4 units.
Incorrect: r2 = 16, so radius is 4 units.

D. Circle I has center at (2, 0) and circle II has center at (0, 2). Both have radius 16 units.
Correct! h = 2, k = 0 in circle I: center (2, 0); h = 0, k = 2 in circle II: center (0, 2). r2 = 16, so radius is 4 units.

If a circle has center at (2, -5) and a radius of 10, which of the following are points on the circle?

A. (12, -5) and (-8, -5)
Correct! (x − 2)2 + (y + 5)2 = 100 and both pairs of coordinates, when put into the equation, generate true statements.

B. (12, -5) and (2, 5)
Incorrect. (x − 2)2 + (y + 5)2 = 100. The first makes the equation true, but not the second pair.

C. (2, 5) and (2, -5)
Incorrect. ( x − 2 )2 + ( y + 5 )2 = 100, the first pair is true, but the second doesn’t make the equation true.

D. (12, -5) and (-2, -15)
Incorrect. ( x − 2 )2 + ( y + 5 )2 = 100 , the first pair makes the equation true, but the second one does not.