| The point (3,5) is the solution to a system of two equations. Which graph could represent this situation? |
 |
 |
 |
 |
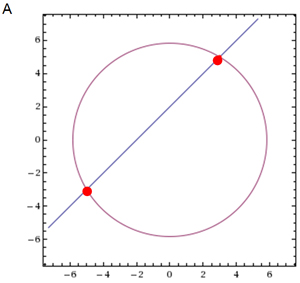
A
Incorrect. The graphs intersect at two points, (-5, -3) and (3,5). There can only be one point of intersection, (3,5).
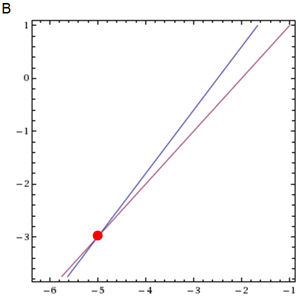
B
Incorrect. Look again, the graphs intersect at one point, but the point of intersection is (-5, -3), The point of intersection has to be (3, 5).
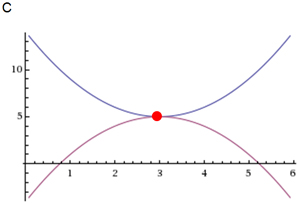
C
Correct! These graphs intersect at only one point and the point of intersection is (3, 5), the given solution.
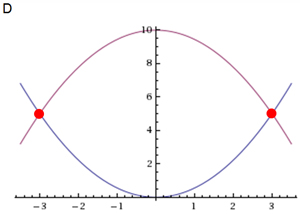
D
Incorrect. The graphs intersects at two points, (-3, 5) and (3,5). The given solution can only intersect at one point (3,5).
Given a system of two equations with exactly two solutions, which of the following statements could be true?
I) The two equations are linear.
II) The two equations are quadratic.
III) The two equations are circular.
A. II only
Incorrect. II could be a possible solution, but it is not the only possible solution. Draw examples of each on a piece of paper to find other correct solutions.
B. III only
Incorrect. III could be a possible solution, but it is not the only possible solution. Draw examples of each on a piece of paper to find other correct solutions.
C. II and III only
Correct! Two quadratic graphs could have exactly two solutions, intersecting exactly twice and two circular graphs could intersect exactly twice. Two lines can never intersect exactly twice. They could never intersect, intersect once or be the same line with infinite intersections.
D. I, II, and III
Incorrect. I is not possible. Two lines can either never intersect, intersect once or intersect an infinite number of times (if they are the same line), causing an infinite number of solutions, but never twice.
| Given (3, 4) is the solution to a system of two linear equations, which of the following could be true of the graphs of these two equations? |
| I) The slope of both lines is 7. |
| II) The slope of one line is 3/7, and the slope of the other line is 2/3. . |
| III) The lines are perpendicular to each other. |
A. II only
Incorrect. II is a correct answer choice, both lines could intersect at the point (3, 4) but it is not the only correct solution. Draw examples of each on a piece of paper to find other correct solutions.
B. III only
Incorrect. II is a correct answer choice, both lines could intersect at the point (3, 4) but it is not the only correct solution. Draw examples of each on a piece of paper to find other correct solutions.
C. II and III only
Correct! Two lines with the same slope will never intersect at one point. If two lines lie in the same plane but have different slopes, they will always intersect at one point.
D. I, II, and III
Incorrect. I is not a possible solution. If two lines have the same slopes the lines are parallel, therefore they will not intersect and not have a solution.
|
The point (-1,1) is the only solution for which system of equations? |
| A. y = x2 and y = 2x2 - 1 |
| B. y = 2x + 3 and 2y = 4x + 6 |
| C. y = -x and y = 2x |
| D. y = -x and x = -1 |
A
Incorrect. By solving the system of equations (substitute the y value x2 from the first equation for the y value in the second equation and solve for x) there will be two answers, (-1,1) and (1,1) instead of only one solution.
B
Incorrect. Notice, if you divide the second equation by 2 it is identical to the first equation resulting in identical graphs. Therefore, they have an infinite number of solutions.
C
Incorrect. Using the solution set substitute in -1 for x in the second equation, y does not equal 1 therefore (-1, 1) is not a solution for the equation y = 2x.
D
Correct! By either graphing the two lines, or by substituting in -1 from the second equation in for the x in the first equation the result is y = 1. The point of intersection is the point (-1,1).
| Each of the following system of equations has no solution except— |
| A. x = 8 and x = 6 |
| B. y = -3 and y = 4 |
| C. y = x2 and y = -x2 - 2 |
| D. y = 3 5 x − 1 and y = 5 3 x + 7 |
A
Incorrect. Both lines are vertical lines, parallel and don’t have a solution.
B
Incorrect. Both lines are horizontal, parallel and don’t have a solution.
C
Incorrect. By graph the two parabolas notice they do not intersect and have no solutions.
D
Correct! Since the lines have different slopes, they must intersect.
Julie drops a rock initially at rest from the top of a 100 foot building at the exact same time Juan throws a rock straight up with an initial velocity of 50 ft/sec. Julie’s rock is modeled by the equation h(t) = 16t2 + 100 and Juan’s rock is modeled by h(t) = -16t2 + 50t, where t is time in the air, and h(t) is vertical height above the ground. Juan and Julie agree the solution set that makes both equations true is (2,36). What does this mean?
A. Two seconds after release, the rocks are on the ground.
Incorrect. Evaluate both functions at t = 2. If both functions equal zero the rocks would be on the ground (vertical position of zero). The equations both equal 36, Julie’s and Juan’s rocks are both 36 feet above ground.
B. Two seconds after release, the rocks are at the same vertical position of 36 ft above the ground.
Correct! The point (2, 36) describes the time t = 2 and height h = 36. Since both equations are satisfied by the points (2, 36), the rocks are both 36 ft above the ground at 2 seconds.
C. Two seconds after release, the rocks are at the same vertical position of 36 ft above Julie’s release point.
Incorrect. Julie drops her rock. It never rises above the release point. Also, the equations find the position above the ground below.
D. After 36 seconds, the rocks are at the same vertical position.
Incorrect. In their equations, time is the independent variable (t = 2) listed in the ordered pair (2, 36).