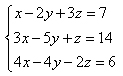What could be a first logical step if solving this system of equations algebraically?

.

A. Add the first and second equations together.
Incorrect. This would not eliminate any of the variables.

B. Multiply the second equation by 4 and the third equation by 5 and add the two new resulting equations together.
Incorrect. This would not eliminate any of the variables.

C. Multiply the first equation by 2 and the third equation by 3 and add the two new resulting equations.
Correct! This would eliminate the z-variables.

D. Multiply the first equation by 3 and add this result to the second equation.
Incorrect. This would not eliminate any of the variables.

Josh was solving the following system:

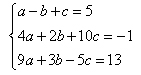
For his first step, Josh chose to multiply the first equation by 2 and add the result to the second equation. What would be a good choice for Josh's second step?

A. Multiply the third equation by 2 and add it to the second equation.
Incorrect. This would eliminate the c-variable, and Josh eliminated the b-variable in his first step.

B. Multiply the first equation by 3 and add the result to the third equation.
Correct! This would eliminate the b-variable.

C. Multiply the first equation by 5 and add the result to the third equation.
Incorrect. This would eliminate the c-variable, and Josh eliminated the b-variable in his first step.

D. Multiply the first equation by 4 and add this result to the second equation.
Incorrect. This would not eliminate any of the variables.

Solve the following system of equations algebraically.

1. (1, -1, 2)
2. 
3. (3, 2, 1)
4. (0, -1, 2)

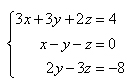
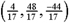
A
Correct! You solved the system.

B
Incorrect. Check your work and try again.

C
Incorrect. Check your work and try again.

D
Incorrect. Check your work and try again.

Find the solution to the system algebraically.

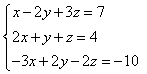
A. (2, 1, -1)
Incorrect. Did you mix up your y and z values?

B. (2, -1, 1)
Correct! You solved the system.

C. (4, 0, 1)
Incorrect. Try again.

D. (4, 1, 0)
Incorrect. Try again.

Solve the following system of equations:

1. (1, 1, -1)
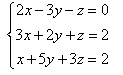
2. (, 0)
3. (2, 0, -4)
4. (-2, 2, 2)

A
Try again.

B
Correct! Great job.

C
Incorrect. Try again.

D
Incorrect. Try again.