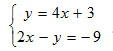
in her calculator and here is the screen she saw after adjusting the ymax.
Jacqui graphed the system
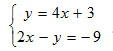
in her calculator and here is the screen she saw after adjusting the ymax.
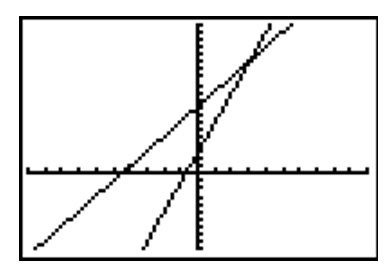
What is the solution to the system?
A. (15,3)
Incorrect. Because the coordinates of the point of intersection are not in the correct (x, y) order.
B. (4, 19)
Incorrect. Because this point is not the point of intersection. The point is on the first equation but not the second.
C. (3, 15)
Correct! This point is the point of intersection for the system and makes both equations true.
D. (2,11)
Incorrect. Because this point is not the point of intersection. The point is on the first equation but not the second.
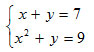 ?
?
A.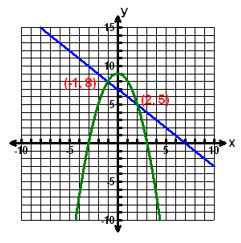 |
C.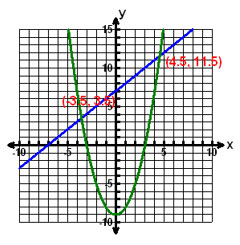 |
B. |
D.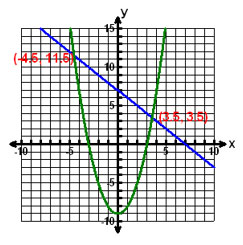 |
A.
Correct! You have correctly graphed both equations in the system and identified the solutions.
B.
Incorrect. You correctly graphed the parabola but made a sign error for the slope in the linear equation.
C.
Incorrect. Because there were errors made in both equations. The slope of the line is negative and the parabola opens downward.
D.
Incorrect. Because the parabola opens downward.
Which graph accurately shows the solution to the system bracketed equations?
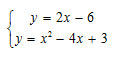
A.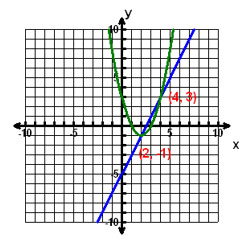 |
C.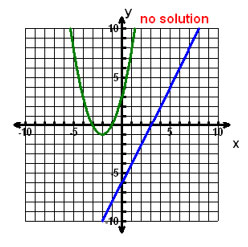 |
B.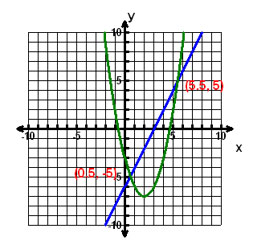 |
D.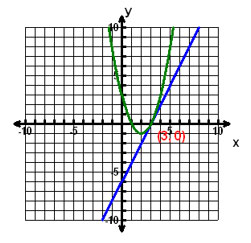 |
A.
Incorrect. Because the line has a y-intercept of -5 instead of -6.
B.
Incorrect. Because the parabola is incorrectly graphed.
C.
Incorrect. Because the parabola is incorrectly graphed.
D.
Correct! You correctly graphed both equations in the system and identified the solution.
Jeff bought 5 daisies and 1 rose from the local florist for $3.25. Andy bought 3 daisies and 3 roses from the same florist for $3.75. Nick decided to use this information to find the cost of each daisy and each rose. He developed the following system to represent the situation.
5d + r = 3.25
3d + 3r = 3.75
where d is the cost of each daisy and r is the cost of each rose.
What is the solution to this system?
A. (0.75, 0.50)
Incorrect. Because the coordinates of the point of intersection are not in the correct (x, y) order.
B. (0.50, 1.25)
Incorrect. Because these prices do not work in either equation.
C. (0.50, 0.75)
Correct! This is indeed the point of intersection for the system and makes both equations true. The cost of each daisy is $0.50 and of each rose is $0.75.
D. (0.75, 1.00)
Incorrect. Because these prices do not work in either equation.