Fredrick wanted to earn some money, but his parents would not let him work for fear that it would interfere with school. He decided to build birdhouses and sell them online. He needed $700 to get tools and to start his webpage. It costs $5.00 for the materials to build each birdhouse. He plans on selling them for $15.00 each, including shipping.

Fredrick determined that the equation y = 700 + 5x represents his business costs and the equation y = 15x represents the income from selling the birdhouses, where y = the amount of money in dollars and x = the number of birdhouses.

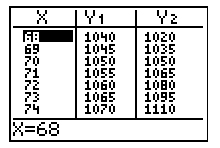
Looking at the following table, how many birdhouses does Fredrick have to sell before he breaks even?

A. 70
Correct! Because both y-coordinates are 1050 when x = 70.

B. 71
Incorrect. Because both y-coordinates are not the same for this one x-coordinate.

C. 73
Incorrect. Because both y-coordinates are not the same for this one x-coordinate.

D. 68
Incorrect. Because both y-coordinates are not the same for this one x-coordinate.

Philip entered a system of equations on his calculator and then went to the table. What is the solution to the system? How does Philip know?

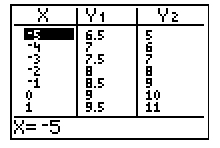
A. There is no solution. None of the y-coordinates is the same as the x-coordinate.
Incorrect. Because in the table there are two y-coordinates that are the same for one x-coordinate indicating that there is a solution.

B. (-4, -3) is the solution because they both have 7 for a y-coordinate.
Incorrect. The solution to a system must be a point of intersection for the two graphs. Remember that both y-coordinates must be the same for this one x-coordinate for the two equations to be equal in value.

C. (0, -1) is the solution because they both have 9 for a y-coordinate.
Incorrect. The solution to a system must be a point of intersection for the two graphs. Remember that both y-coordinates must be the same for this one x-coordinate for the two equations to be equal in value.

D. (-2, 8) is the solution because both y-coordinates are the same for this one x-value.
Correct! You have the correct solution and the correct reason.

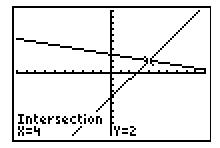
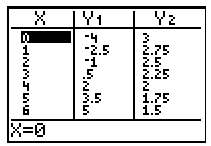
Which of the following tables correctly shows the solution for the given graphed system?

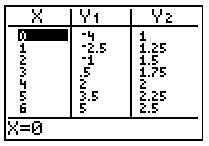
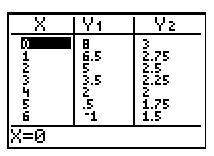
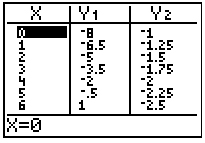
A
Correct! This table correctly shows the solution/point of intersection as (4, 2) and also correctly shows the y-intercepts of both lines as (0, -4) and (0, 3).

B
Incorrect. Although this table correctly shows the solution/point of intersection as (4, 2), it incorrectly shows one of the y-intercepts to be (0, 1). Also, looking at both y-columns, the y-coordinates are increasing in both where the graph shows that one of the lines should have decreasing y-coordinates.

C
Incorrect. Although this table correctly shows the solution/point of intersection as (4, 2), it incorrectly shows one of the y-intercepts to be (0, 8). Also, looking at both y-columns, the y-coordinates are decreasing in both where the graph shows that one of the lines should have increasing y-coordinates.

D
Incorrect. This table shows the solution to be (4, -2) but the solution for the system in the graph is (4, 2).

When Pedro decided to rent a moving truck, he compared the prices from two competing companies. Company A charges $50 for the day and $0.20 per mile that the truck is driven. Company B charges a flat fee of $75 for the day provided that the truck is not driven over 200 miles. Pedro knows that he will need to make several trips back and forth between his new and old homes. Pedro brings out his calculator and inputs the following system and looks at the corresponding table of values.

What mileage would make renting from Company A a better deal for Pedro?

A. 125 miles
Incorrect. At 125 miles, the cost from both companies would be the same so it would not matter from which company Pedro rented the truck.

B. More than 125 miles
Incorrect. Y1 represents Company B and its value of 75 is less than the Y2 values for mileage above 125. That would mean that Company B would be a better deal if driving over 125 miles.

C. Less than 125 miles
Correct! Y1 represents Company B and its value of 75 is more than the Y2 values for mileage under 125. That would mean that Company A would be a better deal if driving less than 125 miles.

D. Cannot be determined from this table.
Incorrect. The break-even point comes when both y-coordinates are the same for one x-coordinate. That happens in this table when x = 125 miles. Comparing the y-coordinates and below the break-even point can determine when one company offers a better deal than the other.

Dimetri was asked to solve the following system:

y = x2 – 6

y = 2(x – 5) + 7

Since both equations were in a calculator-friendly format, he decided to find the solution using the table feature.

What should Dimetri say is the solution to this system of equations?

A. (-1, -5)
Incorrect. Because there are two points within this table where both y-coordinates are the same for its x-coordinate. This answer only gives one of those points.

B. (3, 3)
Incorrect. Because there are two points within this table where both y-coordinates are the same for its x-coordinate. This answer only gives one of those points.

C. (-2, -2) & (2, -2)
Incorrect. Because both y-coordinates are not the same for these two x-coordinates.

D. (-1, -5) & (3, 3)
Correct! Because these are the two points within this table where both y-coordinates are the same for its x-coordinate.