A quadratic function has a vertex of (1, -16) and a y-intercept of -15. Which of the following tables represents this function?

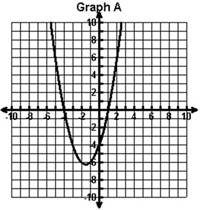
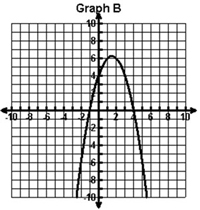
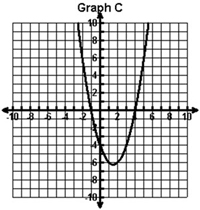
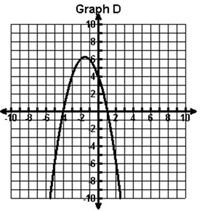
Which of the following graphs shows a quadratic function with roots of – 4 and 1 and a maximum value?

A.	B.
C.	D.

Which of the following graphs contains the points shown in the table below?

A.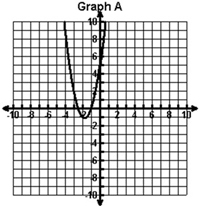	B.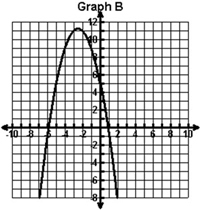
C.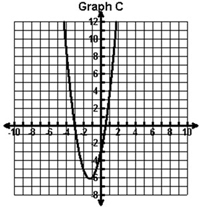	D.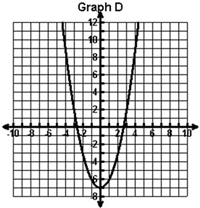

Which of the following functions represents the values in the table below?

1. f(x) = x² + x + 1
2. f(x) = x² − 1
3. f(x) = one-third 1 3 x² − seven-thirds 7 3 x + 2
4. f(x) = 2x² + x − 4

The graph of a quadratic function is shown below.

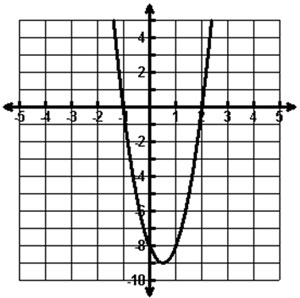
Which of the following is a true statement about the graph?

1. The function has roots at – 1 and 2 and a y-intercept of (0, 8).
2. The function has roots at – 1 and 2 and has a minimum value.
3. The function has roots at – 1 and 2 and has a maximum value.
4. The graph has roots of 1 and – 2 and has a minimum value.

The graph of a quadratic function is shown below.

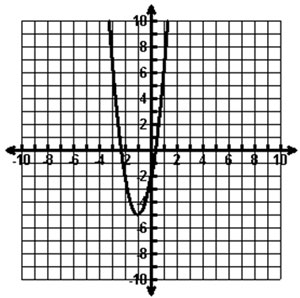
Which of the following tables represents values of the function?

Which of the following graphs represents the function shown below?

f(x) = -(x + 1)² − 3

A.	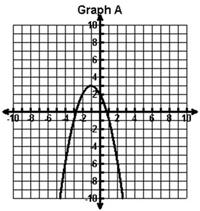B.
C.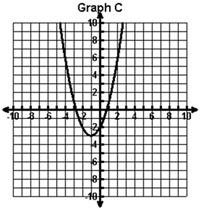	D.

Look at the quadratic function below.

f(x) = 2(x + 3)² − 7

Which of the following is a true statement about the function?

1. The graph of the function has a vertex at (3, -7).
2. The graph of the function has a vertex at (-3, 7).
3. The graph of the function has a vertex at (-3, -7).
4. The graph of the function has a vertex at (3, 7).

Jake is creating a rectangular flower bed in his front yard. He buys a roll of edging to place around the bed. The roll contains 100 feet of edging. The equation y = x(50 − x) can be used to calculate the area of the bed, y, based on the width of the bed, x. The graph of the equation is shown below.

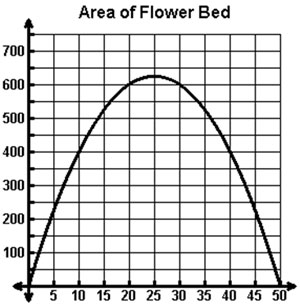
What does the point (20, 600) represent in the situation?

1. A flower bed with a width of 20 feet will take 600 feet to edge.
2. The greatest width of the flower bed can be 20 feet.
3. Jake can build a flower bed with dimensions of 20 feet and 600 feet.
4. A flower bed with a width of 20 feet will have an area of 600 square feet.

A science lab has a variety of cylindrical containers. All the containers have a height of 5 cm, but each has a different radius. The volume of each container, y, can be found using the equation y = 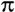x² · 5 where x represents the radius of the base, in cm, of the container. A graph of the equation is shown below.

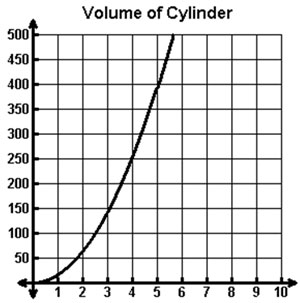
What does the point (8, 1005.3) represent in this situation?

1. A cylindrical container with a radius of 8 cm and height of 5 cm has a volume of 1005.3 cubic cm.
2. A cylindrical container with a diameter of 8 cm and height of 5 cm has a volume of 1005.3 cubic cm.
3. A cylindrical container with a radius and height of 8 cm has a volume of 1005.3 cubic cm.
4. The total volume of 8 cylindrical containers is 1005.3 cubic cm.

A golf ball is hit from ground level with an initial upward velocity of 96 feet/second. The height of the golf ball, y, after x seconds can be modeled by the equation and graph shown below.

y = -16x² + 96x

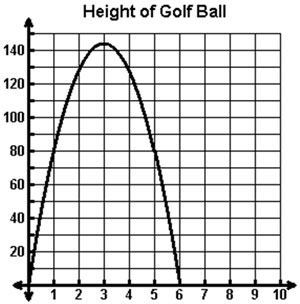
What do the ordered pairs (1, 80) and (5, 80) represent in this situation?

1. At 1 second and again at 5 seconds, the velocity of the golf ball will be 80 feet/second.
2. At 1 second and again at 5 seconds, the golf ball will travel 80 feet along the golf course.
3. At 1 second and again at 5 seconds, the golf ball will reach a height of 80 feet.
4. At a height of 1 foot and again at 5 feet, the velocity of the golf ball will be 80 feet/second.

Which of the following functions has roots of – 1 and – 7?

1. f(x) = x² − 8x + 7
2. f(x) = x² − 8x − 7
3. f(x) = x² + 8x − 7
4. f(x) = x² + 8x + 7

The graph of a quadratic function is shown below.

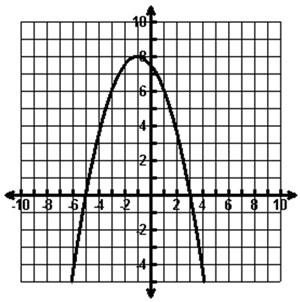
Which of the following functions is shown on the graph?

1. y = one-half 1 2 (x + 5)(x − 3)
2. y = - one-half 1 2 (x − 5)(x + 3)
3. y = - one-half 1 2 (x + 5)(x − 3)
4. y = one-half 1 2 (x − 5)(x + 3)

The graph of a quadratic function is shown below.

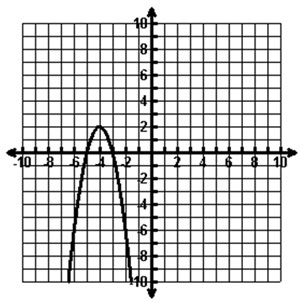
Which of the following is a true statement about the graph of the function?

1. The axis of symmetry is x = 4.
2. The function has no y-intercept.
3. The graph is wider than y = x².
4. The vertex is located at (-4, 2) and is a maximum value.

Which graph has an axis of symmetry of x = 3 and a minimum value of (3, -2)

A.	B.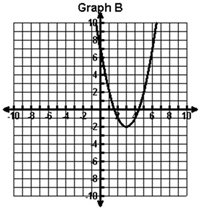
C.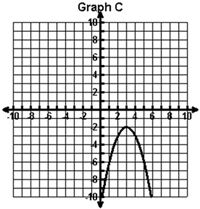	D.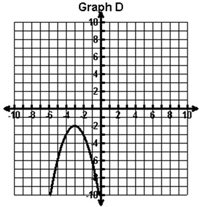

The graph of a quadratic function is shown below.

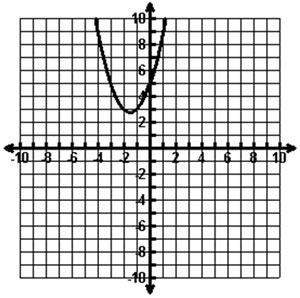
Look at the statements below.

1. The function has a maximum value.
2. The root(s) of the function are imaginary.
3. The graph of the function has a y-intercept of (0, 5).
4. The graph has an axis of symmetry located between x = -1 and x = -2.

Which of the statements above are true about the graph of the function?

1. I, II, III
2. II, III, IV
3. I, III, IV
4. I, II, IV

A quadratic equation is shown below.

y = one-half 1 2 (x − 5)² + 4

Which of the following is NOT true about the graph of the equation?

1. The vertex is located at (5, 4).
2. The graph is wider than y = x².
3. The graph has an axis of symmetry of x = 5.
4. The y-intercept is located at (0, 4).

What are the solution(s) to the equation below?

x² + 6x + 9 = 0

1. – 3 and 3
2. 0
3. -3
4. 9

Shown below is a quadratic function in standard form.

f(x) = x² + 8x − 10

Which of the following is a possible first step in changing the equation to vertex form?

1. f(x) = (x² + 8x + (eight over two 8 2 )² ) − 10 + (eight over two 8 2 )²
2. f(x) = (x² + 8x + (eight over two 8 2 )² ) − 10 − (eight over two 8 2 )²
3. f(x) = (x² + 8x + (8)²) − 10 − (8)²
4. f(x) = (x² + 8x + (8)²) − 10 + (8)²

Shown below is a quadratic function in standard form.

f(x) = 3x² − 12x − 4

Which of the following shows the function in vertex form?

1. f(x) = 3(x − 2)² − 16
2. f(x) = 3(x − 2)² − 8
3. f(x) = 3(x + 2)² − 16
4. f(x) = 3(x + 2)² − 8

Which table below represents a quadratic function?

The vertex form of a quadratic function is shown below.

f(x) = 3(x + 1)² + 4

Which of the following is a possible first step when changing the function to standard form?

1. f(x) = 3(x² + 2x + 2) + 4
2. f(x) = 3(x² + 2x + 1) + 4
3. f(x) = (3x + 3)² + 4
4. f(x) = 3(x + 5)²

The vertex form of a quadratic function is shown below.

f(x) = -2(x − 3)² + 1

Read each of the statements listed below.

Statement 1: The standard form of the function is f(x) = -2x² + 12x − 17.
Statement 2: The graph of the function opens downward.
Statement 3: The vertex of the graph is located at (3, 1).
Statement 4: The axis of symmetry of the graph is x = 3.

Which of the statements are true about the function?

1. 1, 3, 4
2. 2, 3, 4
3. 1, 2, 3, 4
4. 1, 2, 3

Which of the following situations can be modeled using a quadratic function?

1. A baseball is hit with an initial velocity of 80 feet/second. Model the height of the baseball after x seconds.
2. Model the perimeter of a square when given the length of one side, x.
3. Model the volume of a cube when given the measure of one edge, x.
4. A rental car company changes a flat rate for renting a car plus a separate charge per mile. Model the total cost of renting the car for x miles.

The table below shows the length and area of several rectangles. All of the rectangles have a perimeter of 48 inches.

Which of the following functions represents the area of the rectangle, y, based on the length of the rectangle, x.

1. y = x(48 − x)
2. y = 16x + 12
3. y = x(24 − x)
4. y = x²