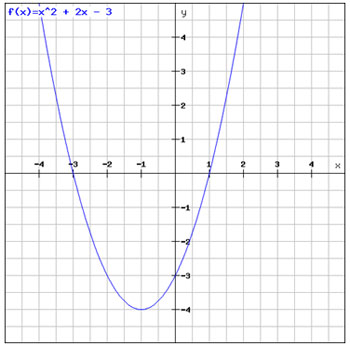
The graph of the quadratic function f(x) = x² + 2x – 3 is shown.

What are the solution(s) to the quadratic function?

A. This quadratic does not have any solutions.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

B. The solutions to this quadratic function are x = -1 and x = 0.
Incorrect. The solutions of the quadratic function are the x-intercepts of the graph.

C. The solutions to this quadratic function are x = 3 and x = 1.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

D. The solutions to this quadratic function are x = 1 and x = -3.
Correct! The solutions to this quadratic function are the x-intercepts of the graph. The solutions are x = 1 and x = -3.

Determine the graph that shows the correct solution(s) to the function
f(x) = -x² + 2x – 1.

A.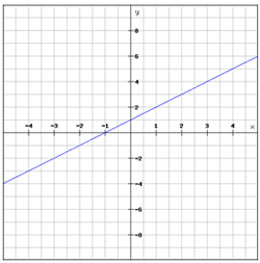	B.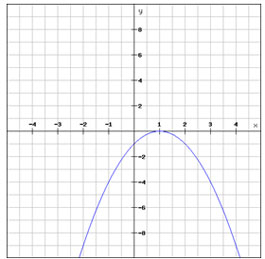
C.	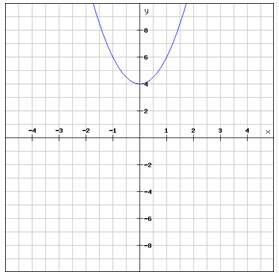D.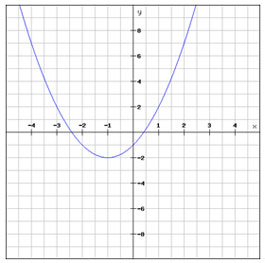

A.
Incorrect. This is the graph of a linear function not a quadratic function.

B.
Correct! This is the graph of the quadratic function. It has only one solution. That solution is x = 1.

C.
Incorrect. This is not the graph of the quadratic function. Since the “a” value is negative the quadratic function opens downwards.

D.
Incorrect. The roots of a quadratic function can be determined by finding the x-intercepts of the graph. The intercepts x = -2.5 and x = 0.5 are not solutions to this quadratic.

The graph of the quadratic function  f(x) = x² + 4 is shown.

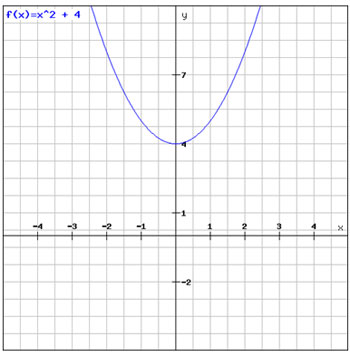
What are the solution(s) to the quadratic function?

A. This quadratic function has no real solutions.
Correct! The graph of this quadratic function has no x-intercepts. Therefore, there are no real solutions.

B. The solutions to this quadratic function are x = -4 and x = 0.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

C. The solution to this quadratic function is x = -4.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

D. The solutions to this quadratic function are x = 4 and x = 0.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

The graph of the quadratic function f(x) = x² – 9 is shown below.

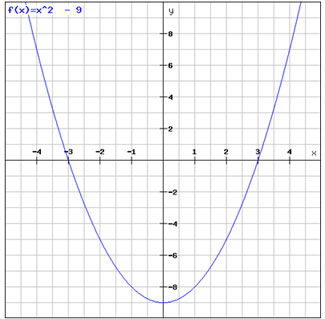
What are the solution(s) to the quadratic function?

A. This quadratic does not have any real solutions.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

B. The solutions to this quadratic function are x = -9 and x = -3.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

C. The solution to this quadratic function is x = -9.
Incorrect. The solutions to a quadratic function can be determined by finding the x-intercepts of the graph.

D. The solutions to this quadratic function are x = 3 and x = -3.
Correct! The solutions to this quadratic function are the x-intercepts of the graph. The solutions are x = 3 and x = -3.

Which of the following quadratic equations does not have solutions that are shown in the graph?

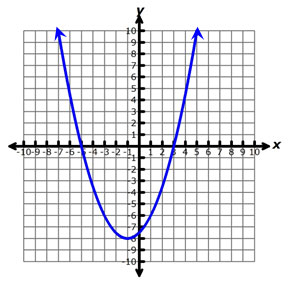
A. 0.5(x – 3)(x + 5) = 0
Incorrect. The solutions of this equation are shown by the points (-5, 0) and (3, 0).

B. 1 2 x² + x - 15 2 = 0
Incorrect. The solutions of this equation are shown by the points (-5, 0) and (3, 0).

C. 1 2 (x – 3)(x + 5) = 4
Incorrect. The solutions of this equation are shown by the points (-6, 4) and (4, 4).

D. 1 2 x² + x – 15 2 = -10
Correct! Because this parabola has a minimum value at y = -8, there are no x-values that will generate a value of -10.

The graph of a quadratic function is shown below.

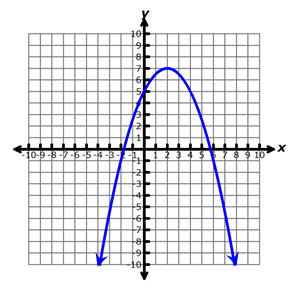
What is the best estimate of the positive value of x for which this function equals 5?

A. 2
Incorrect. This number is the x-coordinate of the vertex of the parabola, but is not the x-coordinate of one of the points (x, 5) that lies on the parabola.

B. 4
Correct!

C. 6
Incorrect. This number is close to the positive value for which this function equals 0.

D. 7
Incorrect. This number is the y-coordinate of the vertex.