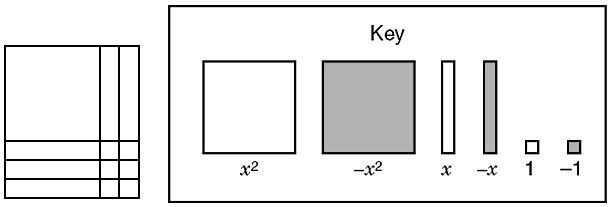
Algebra 1 Module 6 Lesson 5 Assessment Test

The polynomial x² + 5x + 6 is modeled below using algebraic tiles.

What are the solutions to the equation x² + 5x = –6?

A. x = 3 and x = 2	Incorrect. Remember that each factor (x + 3) and (x + 2) must be set equal to 0 to find the solutions to the equation.
B. x = 3 and x = -2	Incorrect. Remember that each factor (x + 3) and (x + 2) must be set equal to 0 to find the solutions to the equation.
C. x = - 3 and x = 2	Incorrect. Remember that each factor (x + 3) and (x + 2) must be set equal to 0 to find the solutions to the equation.
D. x = - 3 and x = -2	Correct! When the factors are (x + 3) and (x + 2) are set equal to zero, the values for x will be -3 and -2

The polynomial x² – 2x – 15 is modeled below using algebraic tiles.

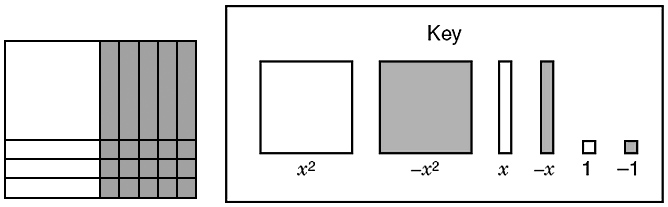
What are the solutions to the equation x² – 2x = 15?

A. x = -5 and x = 3	Incorrect. Remember that each factor (x – 5) and (x + 3) must be set equal to 0 to find the solutions to the equation.
B. x = 5 and x = -3	Correct! When the factors are (x – 5) and (x + 3) are set equal to zero, the values for x will be 5 and 3.
C. x = -5 and x = -3	Incorrect. Remember that each factor (x – 5) and (x + 3) must be set equal to 0 to find the solutions to the equation.
D. x = 5 and x = 3	Incorrect. Remember that each factor (x – 5) and (x + 3) must be set equal to 0 to find the solutions to the equation.

The polynomial 2x² – 9x + 4 is modeled below using algebraic tiles.

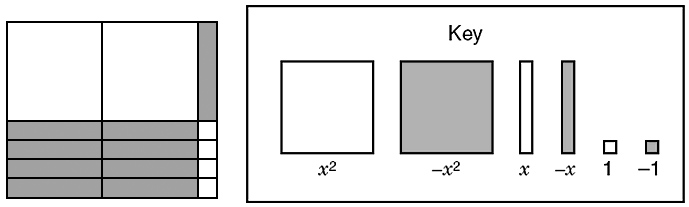
What are the solutions to the equation 2x² – 9x = –4?

A. x = 1 2 and x = 4

B. x = 1 2 and x = –4

C. x = – 1 2 and x = –4

D. x = – 1 2 and x = 4

A. x = ½ and x = 4	Correct! When the factors (2x – 1) and (x – 4) are set equal to 0, the values for x will be 1/2 and 4.
B. x = ½ and x = -4	Incorrect. Remember that each factor (2x – 1) and (x – 4) must be set equal to 0 to find the solutions to the equation.
C. x = -½ and x = -4	Incorrect. Remember that each factor (2x – 1) and (x – 4) must be set equal to 0 to find the solutions to the equation.
D. x = -½ and x = 4	Incorrect. Remember that each factor (2x – 1) and (x – 4) must be set equal to 0 to find the solutions to the equation.

The polynomial x² – x – 12 is modeled below using algebraic tiles.

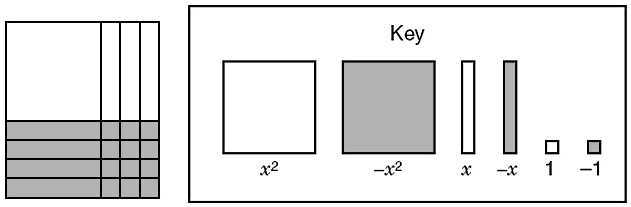
What are the solutions to the equation x² – x = 12?

A. x =3 and x = 4	Incorrect. Remember that each factor (x + 3) and (x – 4) must be set equal to 0 to find the solutions to the equation.
B. x =3 and x = -4	Incorrect. Remember that each factor (x + 3) and (x – 4) must be set equal to 0 to find the solutions to the equation.
C. x = -3 and x = 4	Correct! When the factors (x + 3) and (x – 4) are set equal to 0, the values for x will be –3 and 4.
D. x = -3 and x = -4	Incorrect. Remember that each factor (x + 3) and (x – 4) must be set equal to 0 to find the solutions to the equation.