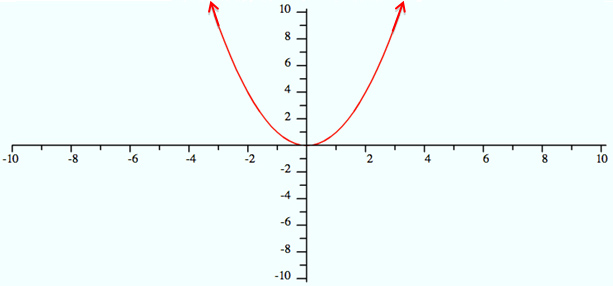
A quadratic function is graphed below. Determine the domain and range of this function.

A. Domain: -∞ < x < ∞
Range: y > 0
Incorrect. The range also includes the value y = 0.

B. Domain: -∞ < x < ∞
Range: y ≥ 0
Correct!

C. Domain: x ≥ 0
Range: y > 0
Incorrect. To determine the domain, identify all of the values of x included in the graph. Notice how the graph continues to extend to the left and right. The range also includes the value y = 0.

D. Domain: -∞ < x < ∞
Range: y < 0
Incorrect. To determine the range, identify all of the values of y included in the graph. The minimum y-value on the graph is 0.

The graph of y = x² + 4 is shown below. Determine the domain and range of this function.

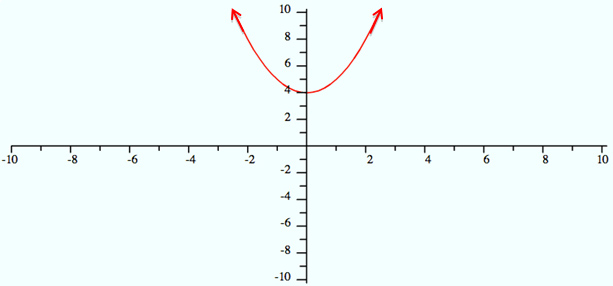
A. Domain: x ≥ 4
Range: -∞ < y < ∞
Incorrect. The domain is the set of all possible x-values in the graph and the range is the set of all possible y-values in the graph.

B. Domain: -∞ < x < ∞
Range: y ≥ 0
Incorrect. To determine the range, identify the set of all possible y-values in the graph. The minimum y-value on this graph is 4.

C. Domain: x ≥ 0
Range: y ≥ 4
Incorrect. To determine the domain, identify the set of all possible x-values in the graph. Notice how the graph continues to extend to the left and right.

D. Domain: -∞ < x < ∞
Range: y ≥ 4
Correct!

The graph of y = -x² – 1 is shown below. What are the domain and range of this function?

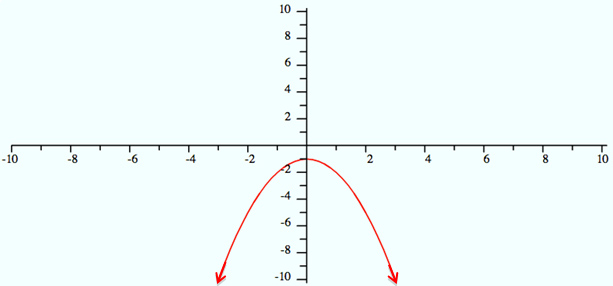
A. Domain: -∞ < x < ∞
Range: y ≤ -1
Correct! The domain of the function y = -x² – 1 is -∞ < x < ∞ and the range is y ≤ -1.

B. Domain: -∞ < x < ∞
Range: y ≥ -1
Incorrect. To determine the range of the function, identify all of the possible y-values on the graph. The maximum y-value is -1.

C. Domain: x ≥ 0
Range: y ≤ -1
Incorrect. To determine the domain of the function, identify all of the possible x-values on the graph. Notice how the graph continues to extend to the left and right.

D. Domain: -∞ < x < ∞
Range: -∞ < y < ∞
Incorrect. To determine the range of the function, identify all of the possible y-values on the graph. The maximum y-value is -1.

A child is standing on a bridge, 64 meters above the ground. The child drops a toy from the bridge. The function f(x) = -16x² + 64 describes the height of the toy in meters after x seconds. The graph of this function is shown below. Identify the domain and range of this function.

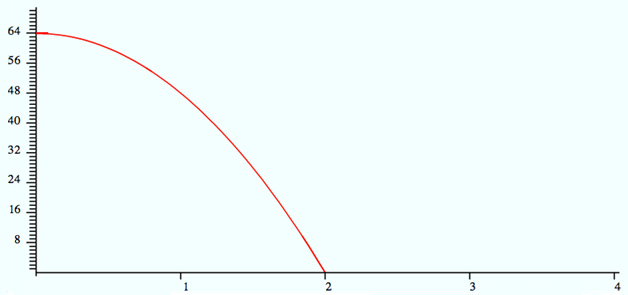
A. Domain: 0 ≤ x ≤ 2
Range: -∞ < y < ∞
Incorrect. To determine the range of the function, identify all of the possible y-values on the graph. The minimum y-value is 0 the maximum y-value is 64.

B. Domain: -∞ < x < ∞
Range: 0 ≤ y ≤ 64
Incorrect. To determine the domain of the function, identify all of the possible x-values on the graph. The minimum x-value is 0 and the maximum x-value is 2.

C. Domain: 0 ≤ x ≤ 2
Range: 0 ≤ y ≤ 64
Correct! The domain of the function f(x) = -4x² + 16 is 0 ≤ x ≤ 2 and the range is 0 ≤ y ≤ 64.

D. Domain: 0 ≤ x ≤ 64
Range: 0 ≤ y ≤ 2
Incorrect. To determine the domain of the function, identify all of the possible x-values on the graph. The minimum x-value is 0 and the maximum x-value is 2. To determine the range of the function, identify all of the possible y-values on the graph. The minimum y-value is 0 the maximum y-value is 64.

Mr. Gavin plans to build a patio with a length of 16 feet and a width of 10 feet. In the middle of his patio, Mr. Gavin plans to build a square koi pond. If each side of the pond measures x feet, the function y = 160 – x² describes the the area of the patio without the pond in square feet. Identify the domain and range of this function.

A. Domain: 0 < x < 10
Range: 60 < y < 160
Correct! The side length of the square pond must be less than the width of the patio. As the side length of the pond increases from 0 to 10, the area of the patio decreases from 160 to 60.

B. Domain: x < 10
Range: 60 < y < 160
Incorrect. The side length of the square pond must be greater than 0.

C. Domain: 0 < x < 10
Range: y < 10
Incorrect. The area of the patio must be less than 160 square feet.

D. Domain: 60 < x < 160
Range: 0 < y < 10
Incorrect. The domain represents the length of the side of the square pond. The range represents the area of the patio, not including the pond.