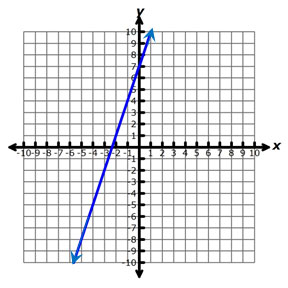
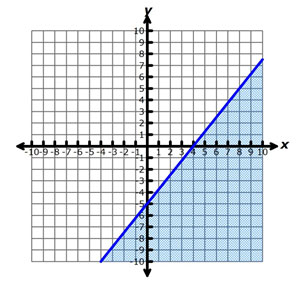
The graph of y = 3x + 7 is shown below.

Which of the following points is not included in the solution set for the inequality y < 3x + 7?

A. (-3, -4)
Incorrect. This point lies in the region beneath the line, so it is a solution to the inequality y < 3x + 7.

B. (-4, -5)
Correct! This point lies on the line, so the coordinates do not represent a set of values that will make the inequality true.

C. (0, 3)
Incorrect. This point lies in the region beneath the line, so it is a solution to the inequality y < 3x + 7.

D. (3, 0)
Incorrect. This point lies in the region beneath the line, so it is a solution to the inequality y < 3x + 7.

Valerie is solving the inequality 3.5x + 5y ≥ -8 for y. Her solution steps are shown below.

Step 1: 3.5x + 5y ≥ −8
Step 2: 5y ≥ -3.5x − 8
Step 3: y ≤ -0.7x – 1.6

In which step did Valerie make her first mistake, and what was that mistake?

A. Step 2. Valerie should have added 3.5x to both sides of the inequality instead of subtracting 3.5x.
Incorrect. In order to solve for y, Valerie needs to use inverse operations in order isolate y.

B. Step 2. Valerie should have divided by 3.5 in order to isolate the variable, x.
Incorrect. Valerie is solving for y, not x. She needs to isolate the y-term by subtracting the x-term from both sides of the inequality.

C. Step 3. Valerie should have subtracted 5 from both sides of the inequality in order to isolate the variable, y.
Incorrect. 5y represents multiplication, and the inverse operation of multiplication is division.

D. Step 3. Valerie was not dividing by a negative number, so she did not need to reverse the inequality symbol.
Correct!

Sharonda makes candles. Red candles cost her $5 to make, and green candles cost her $3 to make. The graph below shows the number of red and green candles that Sharonda can make if she keeps her total production costs at $150.

A. 25 green candles and 20 red candles
Incorrect. This solution represents the point (25, 20), which is above the line and not inside the solution region for the inequality.

B. 20 green candles and 25 red candles
Incorrect. This solution represents the point (20, 25), which is above the line and not inside the solution region for the inequality.

C. 30 green candles and 10 red candles
Correct!

D. 10 green candles and 30 red candles
Incorrect. This solution represents the point (10, 30), which is above the line and not inside the solution region for the inequality.

Which of the following graphs best represents the solution to the inequality 5x – 4y ≤ 20?

A.

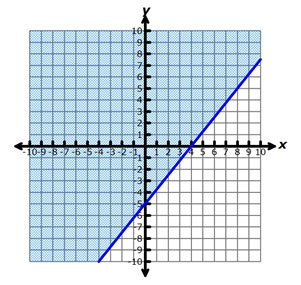
Correct!

B.

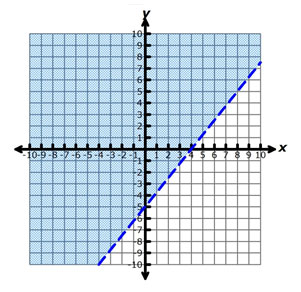
Incorrect. A broken line indicates that the values along the line are not included in the solution set, but the inequality includes "less than or equal to," so the values along the line should be included in the solution set.

C.

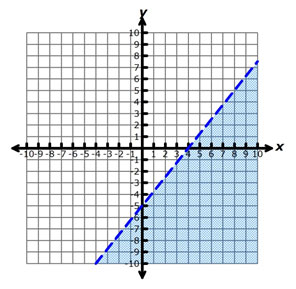
Incorrect. A broken line indicates that the values along the line are not included in the solution set, but the inequality includes "less than or equal to," so the values along the line should be included in the solution set. Also, the values in the shaded region do not make the inequality true.

D.

Incorrect. The values in the shaded region do not make the inequality true. For example, substituting the values (6, 0) into the inequality yields 30 < 20, which is not true.

Which of the following inequalities does not include (3, 12) as a solution?

A. y < 4.5x + 6
Incorrect. When x = 3 and y = 12 is substituted into the inequality, the resulting inequality is true, so (3, 12) is a solution to this inequality.

B. y ≥ 1 3 x + 5
Incorrect. When x = 3 and y = 12 is substituted into the inequality, the resulting inequality is true, so (3, 12) is a solution to this inequality.

C. 2.5x + 4y < 17.5
Correct!

D. 3.2x – 5.2y ≤ -45
Incorrect. When x = 3 and y = 12 is substituted into the inequality, the resulting inequality is true, so (3, 12) is a solution to this inequality.