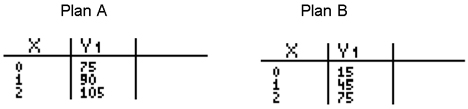
1. At Ivory’s Icee Igloo, Maria makes x pints of cherry Icee, for y dollars. The tables below show the revenue and expenses of her business. How many pints of cherry Icee will she need to sell to break even?
| A. 25 | Incorrect. Find where the Y1 values are the same in both tables. |
| B. 30 | Correct. The revenue and expenses are the same. Maria needs to sell 30 Icees to break even. |
| C. 35 | Incorrect. Find where the Y1 values are the same in both tables. |
| D. 120 | Incorrect. The question is asking for the number of pints,y, when the revenue and expenses are the same. |
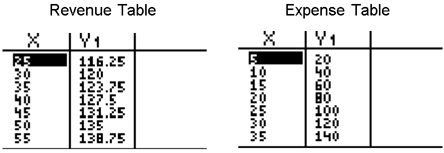
2. Luis is choosing between two International Calling Plans listed below to make business calls to Mexico. The tables represent the relationship between the total cost per month of each plan and the hours of usage.
According to the tables, how many hours would Luis have to talk on each plan to spend the same amount of money?
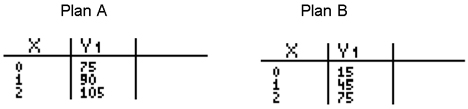
| A. 3 | Incorrect. Find the pattern and continue the pattern on both plans to find the answer. |
| B. 4 | Correct. The pattern was found in both tables and the tables were continued to find at 4 hours the plans cost the same. |
| C. 5 | Incorrect. Plan A increases by $15/hour and Plan B increases $30/hour. |
| D. The calling plans are never the same. | Incorrect. Find the pattern and continue the pattern on both plans to find the answer. |
3. Which of the tables below represents a system of equation that is inconsistent with no solution?
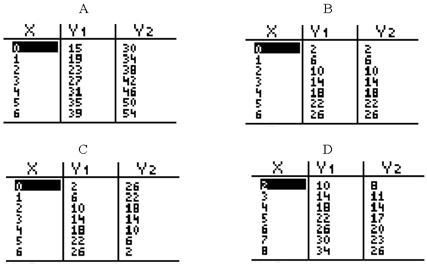
| A | Correct. The slopes are the same and y-intercepts are different. Also, the vertical distance stays the same (Y1-Y2). Thus, the lines are parallel and never intersect. Plotting the points is a good way to double check. |
| B | Incorrect. Slopes are the same, y-intercepts are same, but their vertical distance (Y1-Y2) is 0. Thus, the lines are the same and have infinitely many solutions. This system is consistent and dependent. Plotting the points is a good way to double check. |
| C | Incorrect. Slopes are different and y-intercepts are different. This system has one solution at x = 3. This system is consistent and dependent. Plotting the points is a good way to double check. |
| D | Incorrect. Slopes are the same, y-intercepts (not given) are different, and the vertical distance is getting larger, therefore the intersection must be before x = 2 Actually, if you follow the pattern up, its intersection is at x = -1. This system is consistent and dependent. Plotting the points is a good way to double check. |
4. Between which two x-coordinates in the table does a solution to a system of equations exist?
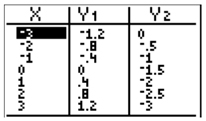
| A. -3 and -2 | Incorrect. Y2 stays higher than Y1. After the intersection, Y1 should be greater than Y2. Plotting the points is a good way to double check. |
| B. -2 and -1 | Correct. Checking the difference in the y-values or plotting points is a good way to find the solution. |
| C. -1 and 0 | Incorrect. Y1 stays higher than Y2. After the intersection, Y2 should be greater than Y1. Plotting the points is a good way to double check. |
| D. 0 and 1 | Incorrect. Y1 stays higher than Y2. After the intersection, Y2 should be greater than Y1. Plotting the points is a good way to double check. |