Which of the following situations cannot be represented by a linear function with a y-intercept that has a positive y-coordinate?
A. The amount of money that Geraldo owes on the
balance of his car loan, y, if he
originally borrowed $6,500 and pays $350 each month for x months.
Incorrect. The y-intercept in this situation is (0, 6,500), which has a positive y-coordinate.
B. The amount of money an employee earns, y, as a function of the number of hours
worked, x, if the pay is $4.50 per
hour.
Correct! The y-intercept in this situation is (0, 0), and the y-coordinate of this point is 0. Zero is not a positive number.
C. The balance of Sheila’s retirement account, y, if she opens the account with $500
and deposits $75 each month for x
months.
Incorrect. The y-intercept in this situation is (0, 500), which has a positive y-coordinate.
D. The altitude of an airplane, y, in feet that takes off an airport as
a function of time, x, since takeoff,
if the runway is at an elevation of 1,100 feet.
Incorrect. The y-intercept in this situation is (0, 1,100), which has a positive y-coordinate.
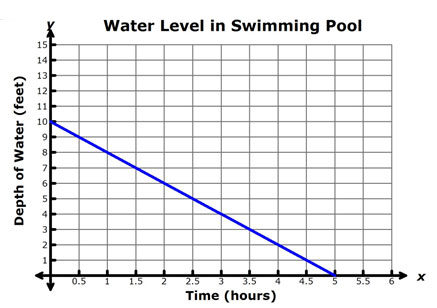
A community pool is being drained for cleaning. The graph below shows the relationship between the depth of water remaining in the pool, y, and the amount of time, x, since the operator began draining the pool.

Which of the following statements is the best interpretation of the x-intercept of the function shown in the graph?
A. The pool will be empty in 5 hours.
Correct!
B. The pool will be empty in 10 hours.
Incorrect. The y-intercept, (0, 10), represents the initial depth of the water in the pool.
C. The water is draining at a rate of 2 feet per hour.
Incorrect. This statement is a good interpretation of the slope, but the question asked for an interpretation of the x-intercept.
D. After 5 hours, the pool will have a depth of 10 feet of water.
Incorrect. The pool begins with an initial depth of 10 feet (this is represented by the y-intercept), and after 5 hours, the pool will have a depth of 0 feet (this is represented by the x-intercept).
Four students’ lunch account balances are shown in the table below.
|
Lunch Account Balances
|
||||
|
Arlene
|
Benjamin
|
Chavon
|
Daniel
|
|
| Monday |
15.00
|
15.00
|
15.00
|
15.00
|
| Tuesday |
12.50
|
12.00
|
11.00
|
12.75
|
| Wednesday |
10.00
|
9.00
|
9.00
|
10.50
|
| Thursday |
7.50
|
6.00
|
7.00
|
8.25
|
| Friday |
5.00
|
3.00
|
5.00
|
6.00
|
If each student continues spending at the same rate as the rate shown in the table, which student will run out of money in their account first?
A. Arlene
Incorrect. Arlene is spending at a rate of $2.50 per day, and will run out of money in 2 days.
B. Benjamin
Correct!
C. Chavon
Incorrect. Chavon is spending at a rate of $2 per day, and will run out of money in 2.5 days.
D. Daniel
Incorrect. Daniel is spending at a rate of $2.25 per day, and will run out of money in 2
2
3
days.
The Art Club is holding a fundraiser to purchase supplies for a ceramics project and has decided to sell cupcakes and chocolate chip cookies. The graph below shows the number of cupcakes and chocolate chip cookies they must sell in order to reach their fundraising goal of $200.
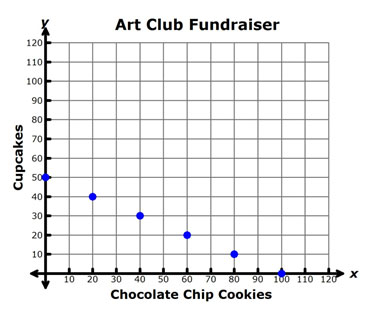
Which of the following numbers best represents the maximum number of chocolate chip cookies that must be sold in order to raise exactly $200?
A. 50
Incorrect. 50 is the maximum number of cupcakes the Art Club must sell in order to raise exactly $200.
B. 100
Correct!
C. 150
Incorrect. This number is the sum of the number of cupcakes (y-intercept) and the number of chocolate chip cookies (x-intercept) that could be sold to raise exactly $200.
D. 200
Incorrect. This number is the fundraising goal.
Three linear functions are shown below.
|
Linear Function II
|
||||
|
x
|
-2
|
0
|
2
|
4
|
|
y
|
3
|
2
|
1
|
1
|
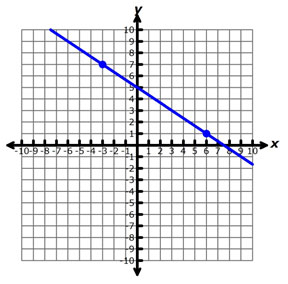
Which of these linear functions has a y-intercept, (0, b), such that 3 < b ≤ 5?
A. I and III only
Incorrect. The y-intercept of Function I is equal to (0, 3), so b = 3. The given criteria state that 3 < b, which does not include 3.
B. I and II only
Incorrect. The y-intercept of Function I is equal to (0, 3), and the y-intercept of Function II is equal to (0, 2). Neither of these values of b lie within the range 3 < b ≤ 5.
C. II and III only
Incorrect. The y-intercept of Function II is equal to (0, 2), so b = 2. The given criteria state that 3 < b, which does not include 2.
D. III only
Correct!