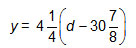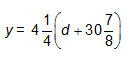Question 1
Mike’s Quick-Tow company charges $25 to hook a vehicle to the tow truck and $1.70 for each mile the vehicle is towed. Which equation best represents the relationship between the number of miles towed, m, and the total cost, c?
Answer Choice |
Correct Answer Feedback |
Incorrect Answer Feedback |
A c = 25 + 1.70 |
|
Incorrect. Mike’s charges 1.70 PER mile, so it should be multiplied by m, the number of miles |
B c = 25 + 1.70m |
Correct! The $25 fee plus the charge per mile, $1.70m, will equal the total cost, c. |
|
C c = 25m + 1.70m |
|
Incorrect. The $25 charge is NOT per mile. It is a one-time charge and should not be multiplied by the number of miles. |
D c = 25m + 1.70 |
|
Incorrect. The $25 charge is NOT per mile. It is a one-time charge and should not be multiplied by the number of miles. |
Question 2:
Andrew is purchasing a new laptop for $1,075, including tax and interest. He will pay for the laptop with monthly payments of $125. If Andrew has made m payments, which equation best describes b, the amount of the remaining balance?
Answer Choice |
Correct Answer Feedback |
Incorrect Answer Feedback |
A b = (1,075 − 125)m |
|
Incorrect. You are close, but the number of payments, m, should be multiplied by $125. |
B b = 125m - 1075 |
|
Incorrect. The balance, $1075, would be decreasing by $125 each month. |
C b = 1075 − 125m |
Correct! The starting balance is $1075 and is decreasing by 125 each month. |
|
D b = 125m + 1075 |
|
Incorrect. The balance, $1075, would be decreasing by $125 each month. |
Question 3
An airplane can travel at an average speed of 300 miles per hour, and the airline allows for 30 minutes of taxiing time at the departure airport and the arrival airport. What equation relates the distance between the two cities, d, to the amount of time, t, it takes for the airplane to depart one gate and arrive at the next gate?
Answer Choice |
Correct Answer Feedback |
Incorrect Answer Feedback |
A d = 300t – 30 |
|
Incorrect. The airplane spends 30 minutes not traveling at the average speed of 300 miles per hour, so that 30 minutes needs to be subtracted before multiplying by the average speed. |
B d = 300t + 30 |
|
Incorrect. The 30 minutes of taxiing time should be subtracted from the total amount of time to determine the amount of time the airplane spends in flight. |
C d = 300(t + 30) |
|
Incorrect. The 30 minutes of taxiing time should be subtracted from the total amount of time to determine the amount of time the airplane spends in flight. |
D d = 300(t – 30) |
Correct! |
|
Question 4
A bolt holds 30 7 8 yards of fabric. Mrs. Fabrese wants to make dresses that require 4 1 4 yards of fabric each. Which equation can Mrs. Fabrese use to determine the number of yards, y, remaining on the bolt of fabric after making a certain number, d, of dresses?
Answer Choice |
Correct Answer Feedback |
Incorrect Answer Feedback |
|
A. y = 30
7
8
– 4
1
4
d |
Correct! |
|
|
B. y = 30
7
8
+ 4
1
4
d |
|
Incorrect. What is the starting amount for the amount of fabric on a bolt? What is the rate of change, per dress, of the amount of fabric remaining on the bolt? |
C.
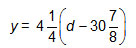
|
|
Incorrect. What is the starting amount for the amount of fabric on a bolt? What is the rate of change, per dress, of the amount of fabric remaining on the bolt? |
D. 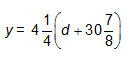
|
|
Incorrect. 30
7
8
yards is the amount of fabric on the full bolt, but this initial amount does not need to be
multiplied by the amount of fabric used for each dress. |
Question 5
Which of the following situations could not be represented with the function, y = 38.7 + 7.4x?
Answer Choice |
Correct Answer Feedback |
Incorrect Answer Feedback |
A. A gasoline tank holds 38.7 gallons of gasoline and Murphy burns 7.4 gallons of gasoline each time he drives to work and back home. What is the number of gallons of gasoline, y, remaining in the tank after Murphy makes x number? |
|
Incorrect. This situation can be represented using the given function. This situation represents a decreasing rate of -7.4 gallons per trip with a starting point of 38.7 gallons. |
B. Mari is training for a bicycle race. She wants to ride a total of 38.7 miles. Each lap around her neighborhood is a combined distance of 7.4 miles. What is the number of miles, y, remaining for Mari to ride after she has completed x laps around her neighborhood? |
|
Incorrect. This situation can be represented using the given function. This situation represents a decreasing rate of -7.4 miles per lap with a starting point of 38.7 miles. |
C. Steve has a weekly lunch budget of $38.70. His favorite restaurant has a special lunch menu with meal combinations for $7.40. What is the amount of money, y, remaining in Steve’s weekly lunch budget after he has purchased x number of lunch meal combinations? |
|
Incorrect. This situation can be represented using the given function. This situation represents a decreasing rate of -$7.40 per lunch meal combination with an initial amount of $38.70. |
D. A crate contains 38.7 pounds of oranges. Karina can place an additional 7.4 pounds of oranges in the crate per hour from her orchard. What is the total weight of oranges, y, in the crate after x hours? |
Correct! This situation represents an increasing rate of 7.4 pounds per hour. An increasing rate of change is represented with a positive number (plus sign), not a negative number (minus sign). |
|