Cupcake Haven is a popular cupcake bakery in Dallas. The owner of Cupcake Haven determined the cost, C, of baking cupcakes daily is:

C = 1500 + 0.2N

where the cost to make one cupcake is $0.20, N is the number of cupcakes and $1500 is an average daily cost for operating the bakery. Select the best description for the function.

A. The linear function is in the first quadrant with a constant of 0.2, the number of cupcakes baked daily is the independent variable and the total cost is the dependent variable.
Incorrect. The average daily cost of 1500 is the constant.

B. The average daily cost is constant, the total cost is the independent variable and the number of cupcakes baked daily is the dependent variable. This is a linear function in the first quadrant with a slope of 0.2.
Incorrect. The independent and dependent variable are reversed.

C. The average daily cost of 0.2 is constant, the number of cupcakes baked daily is the independent variable and the total cost is the dependent variable.
Incorrect. The average daily cost is constant but it is not 0.2.

D. The linear function is in the first quadrant with a slope of 0.2. The average daily cost is the constant, the number of cupcakes baked daily is a positive independent variable and the total cost is the dependent variable.
Correct! The equation supports this conclusion. The constant is 1500; the slope is 0.02, N is the independent variable and C is the dependent variable.

Ellie is driving her car from Austin to Mission, Texas at a constant speed of 55 miles per hour. The distance equation is d = 55t where t is the time and d is the distance. Select the best description for the function.

A. The linear function is in the first quadrant with a slope of 55. Time, the t value, is the independent variable and the distance, the d value, is the dependent variable.
Correct! There isn’t a constant value in this equation, 55 is the slope. The changing values are both positive since time is never negative therefore the graph is in the first quadrant.

B. The linear function is in the first quadrant with a slope of 55. The d value is the independent variable and the t value is the dependent variable.
Incorrect. The independent and dependent variable are reversed.

C. This is a linear function in the first quadrant and the constant is 55. The time is the independent variable and the distance is the dependent variable.
Incorrect. There isn’t a constant, 55 is the slope.

D. The quadratic function is in the first quadrant opening up. The time or t value is the independent variable and the distance, the d value, is the dependent variable.
Incorrect. This is a linear function.

Jose uses his bicycle cab to drive fans to the Astros baseball game. He charges $5 plus $.50 per mile. Jose starts transporting fans 2 hours before the game and continues until 2 hours after the game for a total of approximately 7 hours. Describe the functional relationship.

A. The function is linear. The constant is 7 hours, the slope is 2, the positive number of miles is the independent variable and the total charge is the dependent variable.
Incorrect. The hours mentioned are not part of the function.

B. The function is linear. The constant is 7 hours, the slope is $0.50, the positive number of miles is the independent variable and the total charge is the dependent variable.
Incorrect. The constant is the $5 charge.

C. The function is linear and the constant is the $5 charge, the slope is $0.50, the positive number of miles is the independent variable and the total charge is the dependent variable.
Correct! It is a linear function with a constant of $5, independent variable of miles and the dependent variable is the total charge. The number of hours limits the amount of time he works but not the total charge for the ride.

D. The function is linear. The constant is the $0.50 charge per mile, the slope is $5, the positive number of miles is the independent variable and the total charge is the dependent variable.
Incorrect. The constant is the $5.

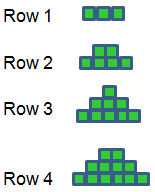
Each row of students was given a designated number of blocks determined by the row they sat in. The individuals in each row created a pattern with the blocks. Determine the functional relationship between the rows and the number of blocks then describe the function completely.

A. There isn’t a function related to the rows and blocks.
Incorrect. The first row has three blocks, the second has 2 x 3 blocks, the third row has 3 x 3 blocks and the fourth row has 4 x 3 blocks.

B. The function is three times the row the blocks are in. The independent variable is the row number and the dependent variable is the number of blocks in the row. This is a linear function with a slope of three located in the first quadrant.
Correct! The first row has three blocks, the second has 2 x 3 blocks, the third row has 3 x 3 blocks and the fourth row has 4 x 3 blocks. In order to determine the number of blocks the row was given the number of the row is needed, the independent variable.

C. The function is three times the row the blocks are in. The independent variable is the number of blocks in the row and the dependent variable is the row number. This is a linear function with a slope of three located in the first quadrant.
Incorrect. The independent and dependent variable are reversed.

D. The function is three plus the row the blocks are in. The independent variable is the row number and the dependent variable is the number of blocks in the row.
Incorrect. The first row has three blocks, the second has 2 x 3 blocks, the third row has 3 x 3 blocks and the fourth row has 4 x 3 blocks.