Another type of congruence transformation is a translation. A translation is a transformation in which a polygon, or other object, is moved along a straight-line path across a coordinate or non-coordinate plane. Translations do not change the size, shape, or orientation of a figure; they only change the location of a figure.

In this section of the resource, you will investigate translations that are performed on the coordinate plane.

Click on the interactive sketch below to perform coordinate translations. Use the buttons labeled “New Square,” “New Parallelogram,” and “New Triangle” to generate a new polygon on the coordinate plane. Use the box containing the translate button to indicate the direction of the translation.

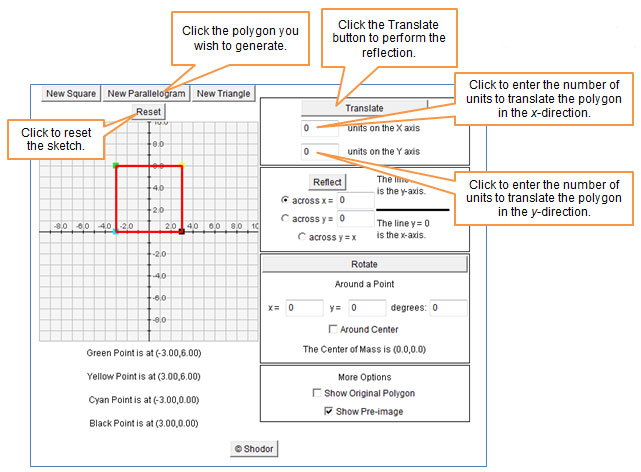
Click to seeInteractive popup. Assistance may be required. additional instructions in using the interactive sketch.

Use the interactive sketch to complete the following table. Reset the sketch and place a new parallelogram on the coordinate grid. Make a copy of the table and paste it into your notes. Fill in the columns for Original Coordinates. Translate your parallelogram according to the direction of translation, then record the reflected coordinates. Repeat a reflection for a second new parallelogram.

Point	Direction of Translation	Original Coordinates	Translated Coordinates
Green	3 units along x-axis 2 units along y-axis	(1, 6)	(4, 8)
Yellow		(2, 0)	(5, 2)
Cyan		(5, 6)	(8, 8)
Black		(6, 0)	(9, 2)
Green	−4 units along x-axis −3 units along y-axis	(−3, −3)	(−7, −6)
Yellow		(−2, −7)	(−6, −10)
Cyan		(3, −3)	(−1, −6)
Black		(4, −7)	(0, −10)

Use your completed table to answer the questions that follow.

How do the x-coordinates of the translated coordinates compare to the x-coordinates of the original coordinates and the direction of translation?

Interactive popup. Assistance may be required. Check Your Answer

The x-coordinates of the translated coordinates are equal to the sum of the x-coordinates of the original coordinates and the direction of translation in the x-direction.

How do the y-coordinates of the translated coordinates compare to the y-coordinates of the original coordinates and the direction of translation?

Interactive popup. Assistance may be required. Check Your Answer

The y-coordinates of the translated coordinates are equal to the sum of the y-coordinates of the original coordinates and the direction of translation in the y-direction.

How does the sign of the translation affect the direction of the translation?

Interactive popup. Assistance may be required. Check Your Answer

For a translation along the x-axis, a positive translation is to the right, and a negative translation is to the left.
For a translation along the y-axis, a positive translation is upward, and a negative translation is downward.

How could you express a translation of h units in the x-direction and k units in the y-direction using an algebraic rule?

Interactive popup. Assistance may be required. Check Your Answer

If a polygon is translated h units in the x-direction and k units in the y-direction, the coordinates of each vertex of the polygon are changed by the following rule:
(x, y) → (x + h, y + k)

Practice

Hexagon ADVERB has coordinates at A (−3, 2), D (1, 3), V (4, 8), E (7, 2), R (3, −2), and B (−3, −4).

1. If the hexagon is translated 3 units to the left and 4 units down, which points will lie in Quadrant III?

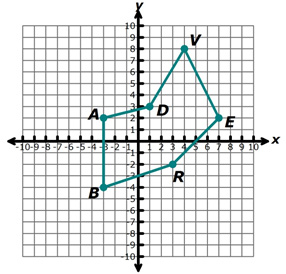
Interactive popup. Assistance may be required. Hint Quadrant III is the lower left quadrant of the coordinate plane, where the x-values are negative and the y-values are negative.

Interactive popup. Assistance may be required. Check Your Answer Points A', D', and B'

2. What would be the coordinates of Point V' if hexagon ADVERB is translated 5 units to the right and 7 units down?

Interactive popup. Assistance may be required. Hint A translation to the right increases the x-coordinates, and a translation down decreases the y-coordinates.

Interactive popup. Assistance may be required. Check Your Answer V' (9, 1)

3. Identify the new coordinates of Points R' and B' if hexagon ADVERB is translated according to the rule (x, y) → (x – 4, y + 5).

Interactive popup. Assistance may be required. Hint A translation in the negative x-direction is to the left, and a translation in the positive y-direction is upward.

Interactive popup. Assistance may be required. Check Your Answer R' (−1, 3), B'(−7, 1)