
In the previous section, you investigated coordinate dilations. Dilations are transformations that preserve the shape of a polygon or an object, but the size changes. Reflections are congruence transformations. That is, a reflection is a transformation that preserves both size and shape of a polygon or object. In this section of the resource, you will investigate reflections that are performed on the coordinate plane.
Use the interactive link shown below to investigate coordinate reflections. Reflect a square, a parallelogram, and a triangle. Reflect these objects across the x-axis, the y-axis, and the line y = x. Once you have done so, use your experiences to answer the questions that follow.

![]()
Click on the sketch below to access the interactive and perform coordinate reflections.
Click to seeInteractive popup. Assistance may be required.
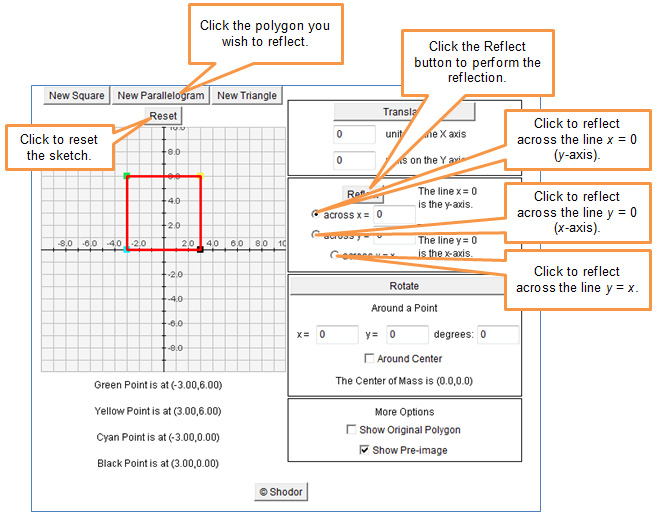
 in using the interactive sketch.
in using the interactive sketch.
Use the interactive sketch to complete the following table. Reset the sketch and place a new parallelogram on the coordinate grid. Make a copy of the table and paste it into your notes. Fill in the columns for Original Coordinates. Translate your parallelogram across the x-axis and then record the reflected coordinates. Repeat a reflection for a second new parallelogram.
Reflect Across |
Original Coordinates |
Reflected Coordinates |
Green |
|
|
Yellow |
|
|
Cyan |
|
|
Black |
|
|
Green |
|
|
Yellow |
|
|
Cyan |
|
|
Black |
|
|
Reflect Across |
Original Coordinates |
Reflected Coordinates |
Green |
(1, 6) |
(1, −6) |
Yellow |
(2, 0) |
(2, 0) |
Cyan |
(5, 6) |
(5, −6) |
Black |
(6, 0) |
(6, 0) |
Green |
(−3, −3) |
(−3, 3) |
Yellow |
(−2, −7) |
(−2, 7) |
Cyan |
(3, −3) |
(3, 3) |
Black |
(4, −7) |
(4, 7) |

Use your completed table to answer the questions that follow.
What patterns do you observe in the coordinates?
Interactive popup. Assistance may be required.
The x-coordinate of the reflected coordinates remain the same as the x-coordinate of the original coordinates.
The y-coordinate of the reflected coordinates has the opposite sign as the y-coordinate of the original coordinates. 
How could you express that relationship using an algebraic rule?
Interactive popup. Assistance may be required.
If a polygon is reflected across the x-axis, the coordinates of each vertex of the polygon are changed by the following rule:
(x, y) → (x, -y) 
Use the interactive sketch to complete the following table. Reset the sketch and place a new parallelogram on the coordinate grid. Make a copy of the table and paste it into your notes. Fill in the columns for Original Coordinates. Reflect your parallelogram across the y-axis and then record the reflected coordinates. Repeat a reflection for a second new parallelogram.
Reflect Across |
Original Coordinates |
Reflected Coordinates |
Green |
|
|
Yellow |
|
|
Cyan |
|
|
Black |
|
|
Green |
|
|
Yellow |
|
|
Cyan |
|
|
Black |
|
|
Reflect Across |
Original Coordinates |
Reflected Coordinates |
Green |
(1, 6) |
(−1, 6) |
Yellow |
(2, 0) |
(−2, 0) |
Cyan |
(5, 6) |
(−5, 6) |
Black |
(6, 0) |
(−6, 0) |
Green |
(−3, −3) |
(3, −3) |
Yellow |
(−2, −7) |
(2, −7) |
Cyan |
(3, −3) |
(−3, −3) |
Black |
(4, −7) |
(−4, −7) |

Use your completed table to answer the questions that follow.
What patterns do you observe in the coordinates?
Interactive popup. Assistance may be required.
The x-coordinate of the reflected coordinates has the opposite sign as the x-coordinate of the original coordinates.
The y-coordinate of the reflected coordinates remain the same as the y-coordinate of the original coordinates. 
How could you express that relationship using an algebraic rule?
Interactive popup. Assistance may be required.
If a polygon is reflected across the y-axis, the coordinates of each vertex of the polygon are changed by the following rule:
(x, y) → (-x, y) 
Use the interactive sketch to complete the following table. Reset the sketch and place a new parallelogram on the coordinate grid. Make a copy of the table and paste it into your notes. Fill in the columns for Original Coordinates. Reflect your parallelogram across the line y = x and then record the reflected coordinates. Repeat a reflection for a second new parallelogram.
Reflect Across |
Original Coordinates |
Reflected Coordinates |
Green |
|
|
Yellow |
|
|
Cyan |
|
|
Black |
|
|
Green |
|
|
Yellow |
|
|
Cyan |
|
|
Black |
|
|
Reflect Across |
Original Coordinates |
Reflected Coordinates |
Green |
(1, 6) |
(6, 1) |
Yellow |
(2, 0) |
(0, 2) |
Cyan |
(5, 6) |
(6, 5) |
Black |
(6, 0) |
(0, 6) |
Green |
(−3, −3) |
(−3, −3) |
Yellow |
(−2, −7) |
(−7, −2) |
Cyan |
(3, −3) |
(−3, 3) |
Black |
(4, −7) |
(−7, 4) |

Use your completed table to answer the questions that follow.
What patterns do you observe in the coordinates?
Interactive popup. Assistance may be required.
The x-coordinate and y-coordinate of the reflected coordinates are the reverse from the x-coordinate and y-coordinate of the original coordinates. 
How could you express that relationship using an algebraic rule?
Interactive popup. Assistance may be required.
If a polygon is reflected across the line y = x, the coordinates of each vertex of the polygon are changed by the following rule:
(x, y) → (y, x)

Pentagon PENTA has coordinates at P (−4, 3), E (0, 7), N (4, 8), T (6, 1), and A (2, −2).
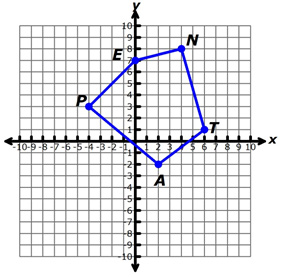
Interactive popup. Assistance may be required. A reflection across the x-axis follows the rule (x, y) → (x, −y).  Interactive popup. Assistance may be required. P' (−4, −3), E'(0, −7), N'(4, −8), T' (6, −1), and A' (2, 2)
Interactive popup. Assistance may be required. P' (−4, −3), E'(0, −7), N'(4, −8), T' (6, −1), and A' (2, 2) 
Interactive popup. Assistance may be required. A reflection across the x-axis follows the rule (x, y) → (-x, y). Interactive popup. Assistance may be required. P' (4, 3), E'(0, 7), N'(−4, 8), T' (−6, 1), and A' (−2, −2)
Interactive popup. Assistance may be required. P' (4, 3), E'(0, 7), N'(−4, 8), T' (−6, 1), and A' (−2, −2)
Interactive popup. Assistance may be required. A reflection across the x-axis follows the rule (x, y) → (y, x). Interactive popup. Assistance may be required. P' (3, −4,), E'(7, 0), N'(8, 4), T' (1, 6), and A' (−2, 2)
Interactive popup. Assistance may be required. P' (3, −4,), E'(7, 0), N'(8, 4), T' (1, 6), and A' (−2, 2) 