Kukulcan Pyramid in Mexico

In the last section, you calculated the volume of a rectangular pyramid using the formula, V = 1 over 3 1 3 Bh, where B represents the area of the base of the pyramid, and h represents the height of the pyramid.

However, as you have seen, not all pyramids are square or rectangular. In this section, you will focus on calculating the volume of triangular pyramids, which are pyramids whose bases are triangles.

Parks and Recreation

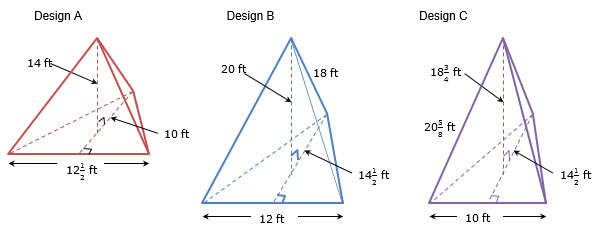
The Parks and Recreation department of a local city wants to build a veterans monument in the shape of a triangular pyramid. The monument cannot exceed a volume of 500 cubic feet. Three designs have been submitted for consideration.

Which of the submitted designs meets the maximum volume requirement?

To solve this problem, use the four-step problem-solving model.

Step 1: Read, understand, and interpret the problem.

  • What information is presented?

    Interactive popup. Assistance may be required.

    Check Your Answer

    Each diagram gives dimensions of a triangular pyramid.
    The volume of a pyramid cannot exceed 500 cubic feet. Close Pop Up
  • What is the problem asking you to find?

    Interactive popup. Assistance may be required.

    Check Your Answer

    You need to determine which of the three triangular pyramids has a volume that is less than or equal to 500 cubic feet. In other words, V ≤ 500. Close Pop Up
  • What information do I not need?

    Interactive popup. Assistance may be required.

    Check Your Answer

    Some of the dimensions in the pyramids may not be necessary. Close Pop Up
Step 2: Make a plan.

  • Use a formula.

    Interactive popup. Assistance may be required.

    Check Your Answer

    For each pyramid, you will need the following formulas:

    Area of a Triangle: A = 1 over 2 1 2 bh

    Volume of a Pyramid: V = 1 over 3 1 3 Bh

    Calculate the volume of each pyramid. Then, determine which pyramids have a volume that is less than or equal to 500 ft3.

    Close Pop Up

Step 3: Implement your plan.

  • What formulas do you need?

    Interactive popup. Assistance may be required.

    Check Your Answer

    Area of a Triangle: A = 1 over 2 1 2 bh

    Volume of a Pyramid: V = 1 over 3 1 3 Bh Close Pop Up
  • What information can you interpret from the diagram, table, or other given information?

    Interactive popup. Assistance may be required.

    Check Your Answer

    For Design A:
    Base of Pyramid:
    b = 121 over 2 1 2 feet
    h = 10 feet
    Height of Pyramid:
    h = 14 feet    		 For Design B:
    Base of Pyramid:
    b = 12 feet
    h = 141 over 2 1 2 feet
    Height of Pyramid:
    h = 20 feet    		 For Design C:
    Base of Pyramid:
    b = 10 feet
    h = 141 over 2 1 2 feet
    Height of Pyramid:
    h = 183 over 4 3 4 feet
    Close Pop Up
  • Solve the problem.

    Interactive popup. Assistance may be required.

    Check Your Answer

    For Design A:
    Area of Base:
    B = 1 over 2 1 2 bh
    B = 1 over 2 1 2 (121 over 2 1 2 ft)(10 ft)
    B = 621 over 2 1 2 ft2     		For Design B:
    Area of Base:
    B = 1 over 2 1 2 bh
    B = 1 over 2 1 2 (12 ft)(141 over 2 1 2 ft)
    B = 87 ft2     		For Design C:
    Area of Base:
    B = 1 over 2 1 2 bh
    B = 1 over 2 1 2 (10 ft)(141 over 4 1 2 ft)
    B = 721 over 2 1 2 ft2
    Volume of Pyramid:
    V = 1 over 3 1 3 Bh
    V = 1 over 3 1 3 (621 over 2 1 2 ft2)(10 ft)
    V = 2081 over 3 1 3 ft3     		Volume of Pyramid:
    V = 1 over 3 1 3 Bh
    V = 1 over 3 1 3 (871 over 2 1 2 ft2)(20 ft)
    V = 5831 over 3 1 3 ft3    		 Volume of Pyramid:
    V = 1 over 3 1 3 Bh
    V = 1 over 3 1 3 (721 over 2 1 2 ft2)(183 over 4 3 4 ft)
    V = 4531 over 8 1 8 ft3


    Designs A and C have volumes that are less than 500 ft3. Close Pop Up
Step 4: Evaluate your answer.

  • Does your answer make sense?

    Interactive popup. Assistance may be required.

    Check Your Answer

    For Design A:
    Area of Base:
    B = 1 over 2 1 2 bh
    B ≈ 1 over 2 1 2 (13 ft)(10 ft)
    B ≈ 65 ft2     		For Design B:
    Area of Base:
    B = 1 over 2 1 2 bh
    B ≈ 1 over 2 1 2 (12 ft)(15 ft)
    B ≈ 90 ft2     		For Design C:
    Area of Base:
    B = 1 over 2 1 2 bh
    B ≈ 1 over 2 1 2 (10 ft)(14 ft)
    B ≈ 70 ft2
    Volume of Pyramid:
    V = 1 over 3 1 3 Bh
    V ≈ 1 over 3 1 3 (65 ft2)(10 ft)
    V ≈ 217 ft3     		Volume of Pyramid:
    V = 1 over 3 1 3 Bh
    V ≈ 1 over 3 1 3 (90 ft2)(20 ft)
    V ≈ 600 ft3    		 Volume of Pyramid:
    V = 1 over 3 1 3 Bh
    V ≈ 1 over 3 1 3 (70 ft2)(20 ft)
    V ≈ 467 ft3
    Close Pop Up
  • Did you answer the question that was asked?

    Interactive popup. Assistance may be required.

    Check Your Answer

    Yes. The question asked which of the three designs have a volume that is less than or equal to 500 cubic feet. Two designs were found meeting this criteria. Close Pop Up
  • Are your units correct?

    Interactive popup. Assistance may be required.

    Check Your Answer

    Yes. Volume has cubic units, and since the original units were feet, the units of the final calculations should be cubic feet.Close Pop Up

Pause and Reflect

How does the four-step problem-solving process help you to solve volume problems?

Interactive popup. Assistance may be required.

Check Your Answer

The four-step problem-solving process provides a structure for a way to think about solving a problem that might seem difficult at first. If you take the problem one step at a time, it isn’t as overwhelming. Close Pop Up

How is calculating the volume of a triangular pyramid different from calculating the volume of a rectangular pyramid?

Interactive popup. Assistance may be required.

Check Your Answer

When calculating the area of the base of the triangular prism, you have to divide the product of the length and width by 2 since the base is a triangle instead of a rectangle.Close Pop Up

Practice

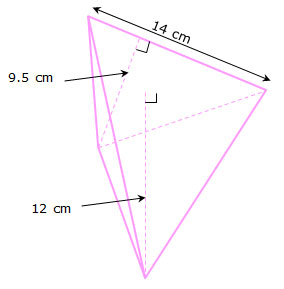
  1. Calculate the volume of the triangular pyramid shown below.
    Interactive popup. Assistance may be required.

    Need a hint?

    The base of this pyramid is a triangle. Which two dimensions are the length and width of the base (i.e., which two dimensions are perpendicular)?Close Pop Up
    Interactive popup. Assistance may be required.

    Check Your Answer

    First, determine the area of the base, B.
    B = 1 over 2 1 2 bh = 1 over 2 1 2 (11.3 cm)(15.1 cm) = 85.315 cm2

    Next, determine the volume of the pyramid, V.
    V = 1 over 3 1 3 Bh = 1 over 3 1 3 (85.315 cm2)(18 cm) = 511.89 cm3

    Close Pop Up
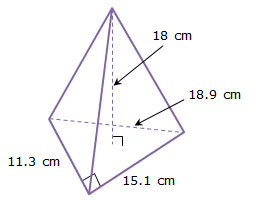
  2. Jennifer has a perfume bottle shaped like a triangular pyramid.

    How much does the bottle hold when it is completely full?

    Interactive popup. Assistance may be required.

    Need a hint?

    The base of this pyramid is a triangle. Which two dimensions are the length and width of the base (i.e., which two dimensions are perpendicular)? Close Pop Up
    Interactive popup. Assistance may be required.

    Check Your Answer

    First, determine the area of the base, B.
    B = 1 over 2 1 2 bh = 1 over 2 1 2 (14 cm)(9.5 cm) = 66.5 cm2

    Next, determine the volume of the pyramid, V.
    V = 1 over 3 1 3 Bh = 1 over 3 1 3 (66.5 cm2)(12 cm) = 266 cm3

    Close Pop Up
  3. A rock crystal in the county geology museum is in the shape of a triangular pyramid. The base is a right triangle with leg lengths of 3 inches and 4 inches. The height of the crystal is 83 over 4 3 4 inches. What is the volume of the rock crystal?

    Interactive popup. Assistance may be required.

    Need a hint?

    The base of the rock crystal is a triangle. Which dimensions are perpendicular so that they can be used as the length and width of the triangle?Close Pop Up

    Interactive popup. Assistance may be required.

    Check Your Answer

    First, determine the area of the base, B.
    B = 1 over 2 1 2 bh = 1 over 2 1 2 (3 in.)(4 in.) = 6 in.2

    Next, determine the volume of the pyramid, V.
    V = 1 over 3 1 3 Bh = 1 over 3 1 3 (6 in.2)(83 over 4 3 4 in.) = 171 over 2 1 2 in.3

    Close Pop Up