Source: Clipboard/Lined Paper, algotruneman, Open Clipart

In this section, you will review numerical expressions that include exponents and prime factorization.

Click on the boxes below to review factorization terms.

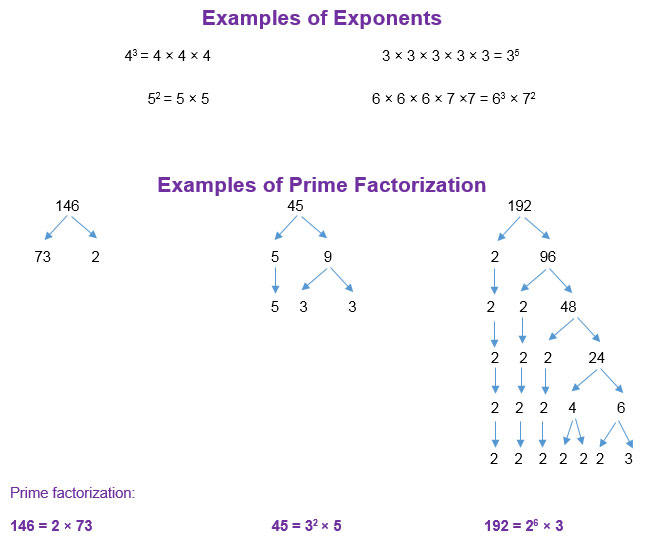
Use the interactive below to review and practice exponents and prime factorization. Match cards that have equivalent expressions.

Using the information from the interactive above, answer the following questions:

• Which pairs of numbers are prime numbers and which pairs are composite numbers?

  Interactive popup. Assistance may be required.

  Need a hint?

  Prime numbers have only factors of 1 and themselves. Composite numbers have factors other than 1 and themselves.
  Interactive popup. Assistance may be required.

  Check Your Answer

  All of the pairs are composite numbers. They all include factors other than 1 and themselves.
• Explain why the prime factorizations used exponents.

  Interactive popup. Assistance may be required.

  Need a hint?

  What do exponents represent?
  Interactive popup. Assistance may be required.

  Check Your Answer

  Exponents can be viewed as a short cut to writing out all the factors. For example: 72 = 2³ × 3² can also be written as 72 = 2 × 2 × 2 × 3 × 3. It is easier and shorter to write the prime factorization of 72 with exponents.

Practice

1. Find the prime factorization for each number.
2. Write it in exponential notation if possible.

1. 300

   Interactive popup. Assistance may be required.

   Need a hint?

   Since 0 is the unit digit, 300 is divisible by 10.
   Interactive popup. Assistance may be required.

   Check Your Answer

   300 = 2 × 2 × 3 × 5 × 5
   300 = 2² × 3 × 5²
2. 195

   Interactive popup. Assistance may be required.

   Need a hint?

   Since 5 is the unit digit, 195 is divisible by 5.
   Interactive popup. Assistance may be required.

   Check Your Answer

   195 = 3 × 5 × 13
   Since there is one of each factor, this cannot be written with exponents.
3. 693

   Interactive popup. Assistance may be required.

   Need a hint?

   Add the digits together. Their sum is divisible by 3, therefore, 693 is divisible by 3.
   Interactive popup. Assistance may be required.

   Check Your Answer

   693 = 3 × 3 × 7 × 11 = 3² × 7 × 11
4. 357

   Interactive popup. Assistance may be required.

   Need a hint?

   Add the digits together to see if their sum is divisible by 3.
   Interactive popup. Assistance may be required.

   Check Your Answer

   357 = 3 × 7 × 17
   Since there is one of each factor, this cannot be written with exponents.